Модуль зубьев зубчатого колеса

Зубчатая передача впервые была освоена человеком в глубокой древности. Имя изобретателя осталось скрыто во тьме веков. Первоначально зубчатые передачи имели по шесть зубьев — отсюда и пошло название «шестерня». За многие тысячелетия технического прогресса передача многократно усовершенствовалась, и сегодня они применяются практически в любом транспортном средстве от велосипеда до космического корабля и подводной лодки. Используются они также в любом станке и механизме, больше всего шестеренок используется в механических часах.

От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.

Скачать Скачать с зеркала

Итак, приступим к графическому построению профиля зубчатого колеса.

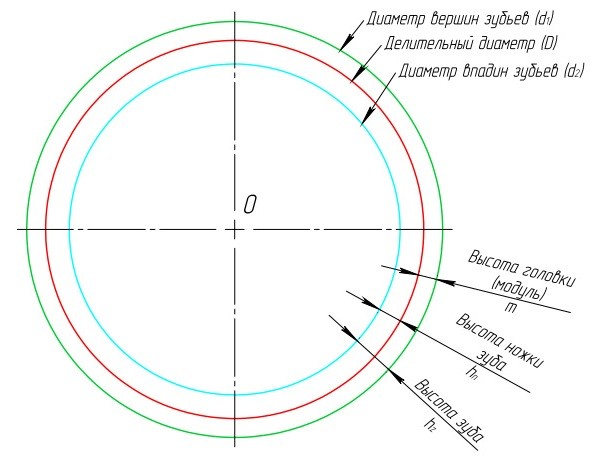
Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
Изобразите диаметр вершин зубьев (d₁) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).

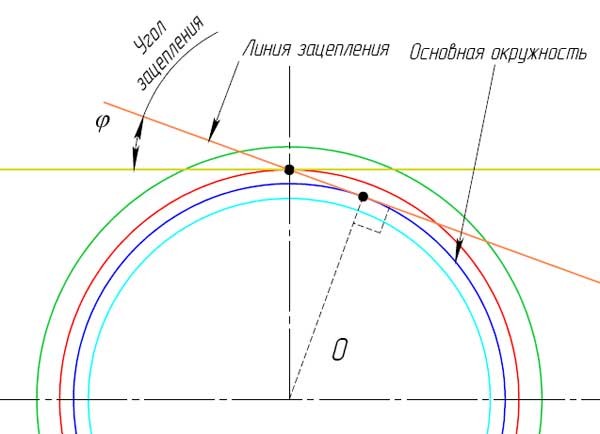
Проведите касательную к делительному диаметру (желтая).
В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.

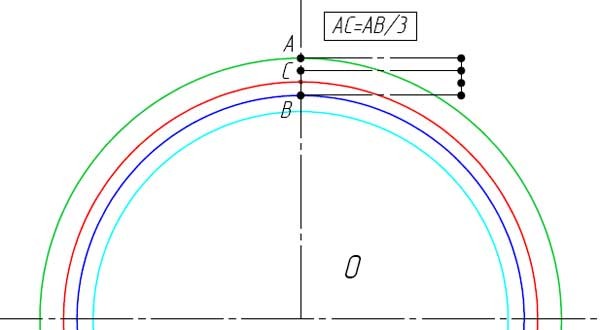
Отметьте точку A на диаметре вершин зубьев.
На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности.
Разделите расстояние AB на 3 части и отметьте, точкой C, полученное значение от точки A в сторону точки B на отрезке AB.

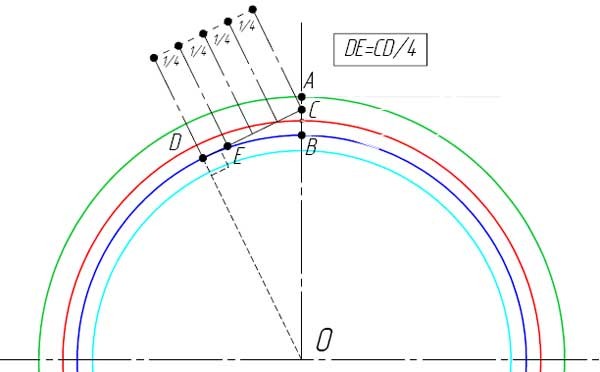
От точки C проведите касательную к основной окружности.
В точке касания отметьте точку D.
Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.

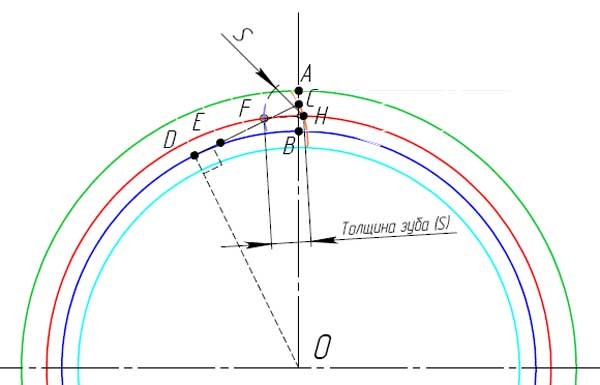
Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.

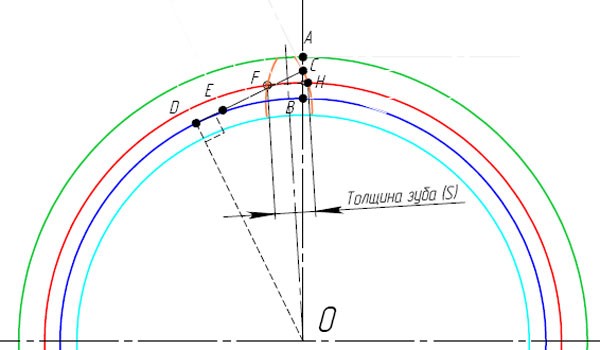
Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.

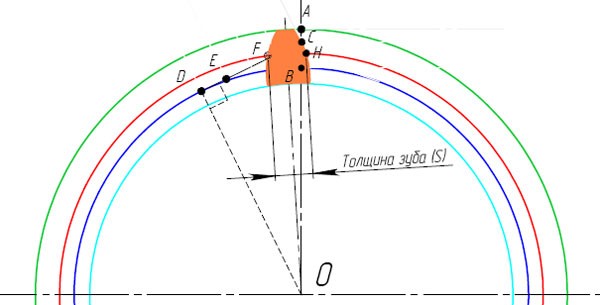
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:

Модуль m=5 мм
Число зубьев z=20
Угол профиля исходного контура ?=20 0

Делительный диаметр D=100 мм
Диаметр вершин зубьевd₁=110 мм
Диаметр впадин зубьевd₂=87.5 мм
Толщина зубьев по делительной окружности S=7.853975 мм

На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.

Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.

P.S.(16.03.2010) Скачать Camnetics GearTrax

А теперь переходим с следующей части урока.

Скачать 2-ю часть урока №30 Скачать с зеркала

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

Расчет шестерен онлайн

Цилиндрические шестерни → Реечная передача

Для преобразования вращательного движения в поступательное и наоборот применяют реечную передачу, которая является частным случаем цилиндрической зубчатой передачи. Рейку рассматривают как зубчатое колесо, диаметр которого увеличен до бесконечности.

ЗАО «НПО «Механик» изготавливает цилиндрические реечные передачи со следующими характеристиками:

— Класс точности — до 6 включительно;

— Модуль — до 30 включительно;

— Длина рейки — до 3 500 мм включительно.

Изготавливаем цилиндрические реечные передачи в штучном и серийном производстве. Возможно изготовление по образцам и эскизам заказчика. Индивидуальный подход.

Реечная передача отличается простотой конструкции, благодаря чему она надежна в эксплуатации. Кроме этого у реечной передачи достаточно высокий КПД (0,94 — 0,98). Составляющие реечной передачи изготавливаются из относительно недорогих углеродистых конструкционных или легированных сталей. К недостаткам реечной передачи можно отнести то, что ее передаточное число равно 1 и поэтому выигрыш в силе отсутствует.

Основной размерный параметр зубчато-реечной передачи — шаг между зубьями рейки. Шаг рейки может рассчитываться по метрической или по модульной системе. В модульной системе расстояние между зубьями рейки рассчитывается по формуле:

m = D/z,

где m — модуль пары рейка-шестерня;
z — количество зубьев шестерни;
D — делительный диаметр шестерни (диаметр окружности, проходящей через полувысоту зуба шестерни; для некорригированных зацеплений начальные и делительные окружности совпадают).

Поскольку значение модуля дробное и представляет собой бесконечную десятичную дробь, для расчетов применяют его округленное значение. В передачах рейка-шестерня используют общепринятые значения модуля в пределах от 0,5 до 25 мм.

Классы точности зубчато-реечной передачи
Класс точности	Накопленная погрешностьна длине 1м, мм
5	0,023
6	0,033-0,040
7	0,06-0,08
8	0,070-0,095
9	0,07-0,10
10	0,22

В метрической системе расстояние между зубьями рейки измеряется в миллиметрах. Метрическая система применяется в случаях, когда по технологии производства передачи зубчатое колесо подбирается под рейку, а модульная — наоборот, когда зубчатая рейка подбирается под шестерню. Модульная система, соответственно, используется преимущественно в производстве комплектных приводов (серийный мотор-редуктор, шестерня, рейка), а метрическая — для решений в области модернизации или построения нестандартных машин и механизмов.

При вращении зубчатого колеса вокруг неподвижной оси зубчатая рейка перемещается прямолинейно-поступательно при каждом обороте колеса на величину S, равную длине начальной окружности зубчатого колеса (в мм), т. е.:

S = π·d = π·m·z,

где d — диаметр начальной окружности зубчатого колеса, мм;
m — модуль зубчатой рейки, мм;
z — число зубьев колеса.

Вместо зубчатой рейки можно заставить перемещаться зубчатое колесо, в этом случае путь пройдет не зубчатая рейка, а ось реечного зубчатого колеса при перекатывании по неподвижной зубчатой рейке.

Зная число оборотов зубчатого колеса в минуту реечной передачи, скорость, с которой перемещается зубчатая рейка, рассчитывают по формуле:

v =π·D·n/1000 = π·m·z·n/1000

где v — скорость перемещения зубчатой рейки, м/мин;

n — число оборотов в минуту зубчатого колеса.

Формулы для расчета реек
Параметры и обозначения	Расчетные формулы
Угол профиля зуба рейки а	а=20°
Угол наклона зуба β	не более 20°
Модуль нормальный m_n	m_nпринимается конструктивно и определяется расчетом
Модуль основной (торцовый) m_t	m_t= m_n/cosβ
Шаг нормальный P_n	Р_n = π·m_n
Шаг торцовый P_t	P_t= Р_n/cosβ
Высота головки зуба, h_a	h_a= m_n
Высота зуба h (размер справочный)	h = 2,25·m_n
Ширина рейки b	b = (2..10) m_n
Длина косого зуба b₁	b₁= b/cosβ
Линейное перемещение рейки L, соответствующее углу поворота колеса	L= Y·P_t z/360°
Угол поворота колеса у, соответствующий перемещению рейки на величину L	у=L·360/ P_t·z

Читайте также Индуктивность проводника

Зубчато-реечные передачи выполняются с прямыми зубьями для работ на малых и средних скоростях, с косыми зубьями для использования на средних и высоких скоростях или когда требуется повышенная точность перемещения.

Базовыми поверхностями рейки называют поверхности, относительно которых задается положение делительной прямой и направление зуба рейки.

По вопросам изготовления реечных передач с прямым и косым зубом обращайтесь в отдел продаж по телефону:

Пробую на калькуляторе онлайн вычислить простой пример 2+2×2, в ответе получаю 8. Может быть калькулятор неправильно считает ?

Калькулятор считает правильно !

Просто при вводе каждого математического действия калькулятор производит промежуточный расчет (подытог). Посмотрите на дисплее текущих действий.

Считаем: 2 + 2 = 4, 4 × 2 = 8. Правильный ответ 8.

Получить в ответе 6 можно используя Математический режим калькулятора. Этот режим поддерживает работу с выражениями и не делает подытог. Настройте математический режим, используя меню под корпусом калькулятора.

Зубчатые передачи стартера

Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в силовых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомобильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличением межосевого расстояния.

Модули зубчатых передач стартеров

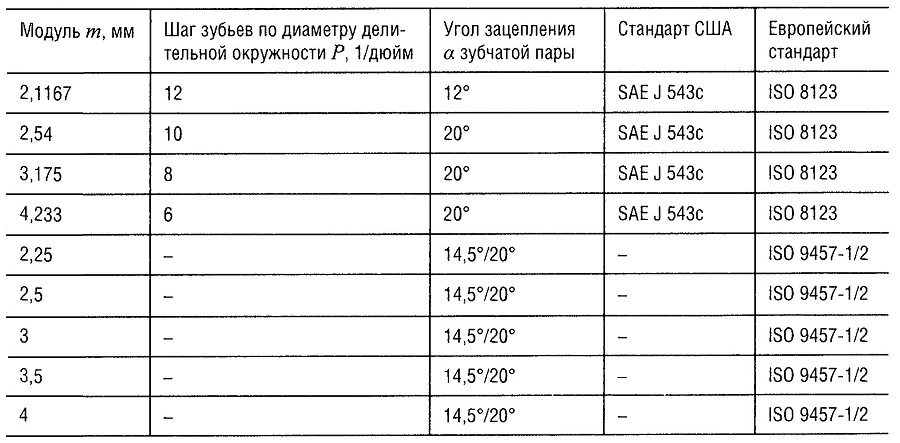
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением. Для шага зубьев принято следующее обозначение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на заготовке, рассчитанной по диаметру на 10 зубьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х. (Это обозначение нельзя смешивать с обозначением Р 8/10, приведенным ниже).

Шаг 4: Делаем зубчатую форму

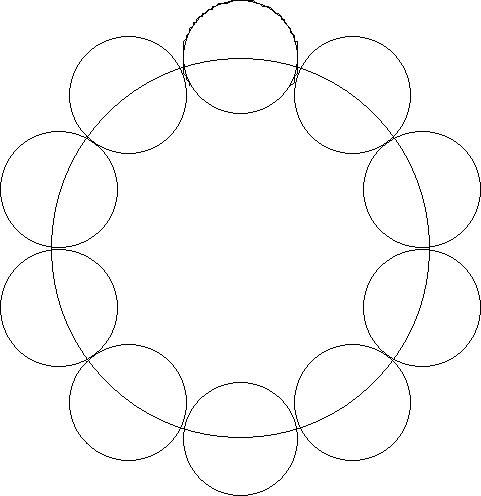
Удалите верхнюю часть одного круга и нижнюю часть следующего круга. Чтобы сделать это, у вас должно быть четное количество зубьев

У нас есть первая шестерня. Она может быть вырезана из дерева или металла с помощью базовых подручных инструментов, пил и напильников.

Этот процесс легко повторить для любого количества шестеренок, которое вам нужно. Держите размер круга по образцу, и они будут соответствовать друг другу.

Шевронные модификации и аналоги с внутренним зацеплением

Шевронные шестерни позволяют справиться с проблемами механической осевой силы. В отличие от прямых и косозубых версий, зубья выполнены в виде литеры V. Осевое воздействие двух половин приспособления компенсируется взаимодействием, что дает возможность избежать применения упорных подшипников на валу. Указанная модель самостоятельно устанавливается по оси, один из рабочих редукторов монтируется на цилиндрических укороченных подшипниках (плавающие опоры).

Модуль шестерни с внутренним зацеплением оснащается зубцами, имеющими нарезку внутри. Эксплуатация детали предполагает односторонние обороты ведущего и ведомого колеса. В такой конструкции меньше затрат уходит на трение, что способствует повышению КПД. Подобные приспособления применяются в механизмах, ограниченных по габаритным размерам, а также планетарных передачах, специальных насосах и танковых башенках.

Обслуживание и расчёт

Техобслуживание заключается в осмотре механизма, проверке целостности зубьев и отсутствия сколов. Проверка правильности зацепления производится при помощи краски, наносимой на зубья. Изучается величина пятна контакта и его расположение по высоте зуба. Регулировка производится установкой прокладок в подшипниковых узлах.

Сначала надо определиться с кинематическими и силовыми характеристиками, необходимыми для работы механизма. Выбирается вид передачи, допустимые нагрузки и габариты, затем подбираются материалы и термообработка. Расчёт включает в себя выбор модуля зацепления, после этого подбираются величины смещений, число зубьев шестерни и колеса, межосевое расстояние, ширина венцов. Все значения можно выбирать по таблицам или использовать специальные компьютерные программы.

Главными условиями, необходимыми для длительной работы зубчатых передач, являются износостойкость контактных поверхностей зубьев и их прочность на изгиб.

Достижению хороших характеристик и уделяется основное внимание при проектировании и изготовлении зубчатых механизмов.

Модуль зубьев зубчатого колеса