Расчёт индуктивности

Расчёт индуктивности. Часть 1

Всем доброго времени суток! В прошлой статье я рассказывал о таком явлении как электромагнитная индукция и ЭДС возникающая при самоиндукции и взаимной индукции. Устройства, в основе которых лежат данные явления и процессы, называются индуктивными элементами (катушки колебательных контуров, трансформаторы, дроссели, реакторы). В качестве одного из основных параметров данных элементов выступает индуктивность L(также имеет название коэффициента самоиндукции). О том, как рассчитать данный параметр пойдёт речь в данной статье.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Свойства

При подаче напряжения к индуктивной катушке, в ней происходит линейное нарастание тока, а при его снятии начинается его падение. Моментально остановить его протекание в катушке не представляется возможным, как, например, нельзя сразу остановить автомобиль, мчащийся на скорости. При попытке быстро остановить нарастание этого параметра, произойдёт удар напряжения, равный тому, что оно, при этом, может вызвать искровой разряд. Подобное явление получило название самоиндукция. На этом принципе основана работа катушки зажигания в автомобиле.

Коэффициент самоиндукции — это есть индуктивность. Иными словами: величина, которая характеризует связь между находящимся в проводнике электрическим током и магнитным полем, создаваемым при протекании. Эта мера представляет сумму потока индукции. Прямая зависимость её от конфигурации проводника и от проницаемости доказана.

При подаче на катушку электрического тока постоянного напряжения, в катушке возникает напряжение, противоположное напряжению электрического тока (Е =U), которое исчезает через некоторое время. Это противоположное напряжение называется ЭДС (электродвижущей силой самоиндукции). Параметр зависит от индуктивности катушки.

ЭДС самоиндукции

Если подавать и снимать напряжение с электрической катушки, то магнитное поле будет появляться, исчезать, появляться, исчезать… В итоге получаем магнитное поле, которое постоянно меняется. Проходя через витки катушки магнитное поле будет индуцировать в ней электродвижущую силу, которая называется ЭДС самоиндукции.

Коэффициент самоиндукции – это величина ЭДС самоиндукции, возникающей при изменении тока в единицу времени. Коэффициент самоиндукции измеряется в Генри (Гн).

Индуктивностью в 1 Генри обладает катушка. В которой при изменении тока на 1 Ампер в 1 секунду возникает ЭДС самоиндукции в 1 Вольт.

Давайте напряжение цепи катушки обозначим через U, результирующее напряжение Uр, а ЭДС самоиндукции Ес, тогда получим следующие формулы:

В момент замыкания цепи результирующее напряжение будет следующим:

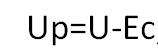
А в момент размыкания цепи:

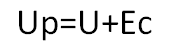
Величина ЭДС самоиндукции может многократно превышать напряжение источника тока. Поэтому при размыкании цепей с большой индуктивностью появляется дуга, и соответственно обгорают контакты.

Об индуктивности простыми словами

Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).

Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.

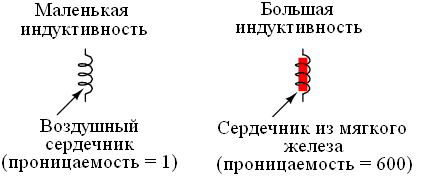
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.

• Ɛ – ЭДС самоиндукции;
• L-индуктивность;
• I – сила тока;
• t – время.

При этом L равно магнитному полю (Ф) деленному на силу тока (I).

Датчики

Изменение напряжения на катушке индуктивности используют для контроля параметров окружающей среды. Такие датчики чутко реагируют на приближение изделий с ферромагнитными свойствами. Их применяют для бесконтактной фиксации положения отдельных частей механизмов, створок ворот и других изделий.

В соответствующем исполнении они хорошо противостоят неблагоприятным внешним воздействиям. Потенциальных потребителей привлекают простота, разумная стоимость, долговечность. Функциональный датчик несложно сделать собственными руками при необходимости. Такие приборы без проблем совмещаются с другими компонентами систем автоматизации.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

где R является собственным сопротивлением обмотки.

Electronov.net | Библиотека

Индуктивность обладает комплексным импедансом (сопротивлением):

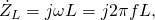
j — мнимая единица;

ω — циклическая частота (рад/с) протекающего синусоидального тока;

f — частота в Гц;

L — индуктивность катушки (Генри).

Комплексный импеданс в общем случае записывается как сумма активного и реактивного сопротивлений:

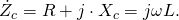
Отсюда следует, что активное сопротивление идеальной индуктивности равно нулю, а реактивное сопротивление равно: 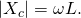Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление равно нулю. Индуктивность по определению численно равна отношению создаваемого током потока магнитного поля, пронизывающего катушку, к силе протекающего тока. Отсюда следует, что применять катушки индуктивности имеет смысл только в цепях переменного тока.

Если Вы не привыкли слепо доверять формулам, то следующий абзац для Вас:

Чтобы разобраться, почему с ростом частоты тока у индуктивности растет реактивное сопротивление, необходимо вспомнить явление самоиндукции, которое можно сформулировать в 2 эквивалентных вариантах:

• Возникновение магнитного потока самоиндукции при протекании по цепи тока;
• Возникновение ЭДС индукции в том контуре, по которому протекает переменный ток.

По Закону электромагнитной индукции Фарадея, ЭДС индукции можно записать как:

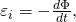
ε_i — величина ЭДС индукции;

Φ — величина магнитного потока.

В случае контура, содержащего N витков, используется понятие потокосцепления Ψ_s самоиндукции (Ψ_s = NΦ_s).

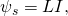
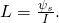
С учетом данных формул, можно записать ЭДС и ток самоиндукции:

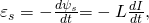
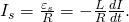
Знак минуса показывает, что направление тока самоиндукции противоположно направлению основного тока.

Из этих формул следует, что любые изменения тока в цепи тормозятся, и тем сильнее, чем больше индуктивность цепи и меньше ее сопротивление.

Если сформулировать по научному:

Правило Ленца для явления самоиндукции – ток самоиндукции препятствует любым изменениям основного тока, текущего по цепи.

Можно также сказать, что индуктивность цепи является мерой ее электрической инертности, подобно тому, как масса в механике является мерой инертности тела при его поступательном движении.

И как Вы уже наверняка догадались, природа реактивного сопротивления индуктивности заключена в явлении ЭДС и тока самоиндукции, а скорость изменения величины тока – это его частота.

Схема замещения не идеальной (реальной) индуктивности:

Сопротивление потерь:

В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля, наблюдаются паразитные эффекты, вследствие которых импеданс катушки не является чисто реактивным. Наличие паразитных эффектов ведет к появлению потерь в катушке, оцениваемых сопротивлением потерь:

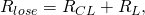
R_CL – диэлектрические потери;

R_L – индуктивные потери.

Диэлектрические потери вызваны магнитными свойствами диэлектрика, а также паразитной емкости, которая образуется между витками, вследствие наличия изоляции обмоточного провода, и соответственно появляются межвитковые утечки и прочие потери, характерные для диэлектриков конденсаторов. Однако для современных катушек общего применения эти потери пренебрежимо малы.

Индуктивные потери складываются из следующих составляющих:

• Потери в проводах:

В свою очередь, потери в проводах вызваны тремя причинами:

• Провода обмотки обладают омическим (активным) сопротивлением.
• Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено поверхностным эффектом (скин-эффектом). Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие, уменьшается полезное сечение проводника и растет сопротивление. Подробнее о поверхностном эффекте можно прочитать [гиперссылка]здесь[/гиперссылка].
• В проводах обмотки, свитой в спираль, проявляется эффект близости (англ. proximity effect), суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля, которые появляются из-за явления взаимной индуктивности, к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведет к дополнительному возрастанию сопротивления провода. Подробнее о эффекте близости можно прочитать [гиперссылка]здесь[/гиперссылка].

• Потери на перемагничивание ферромагнитного сердечника:

Данные потери связаны с эффектом гистерезиса в ферромагнетиках.

• Потери на вихревые токи (токи Фуко):

Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, т.е. витках и сердечнике. При этом возникают вихревые (т.е. замкнутые в кольце) токи — токи Фуко, которые по физической природе ничем не отличаются от индукционных токов, возникающих в линейных проводах. Помимо электрических потерь, вихревые токи также разогревают каркас и обмотку катушки.

Резонансная частота индуктивности:

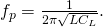
При f > f_р катушка индуктивности в цепи переменного тока ведет себя как конденсатор. Следовательно, индуктивность целесообразно использовать лишь на частотах f Страниц: 1 2 3

Формула индуктивности

Имеется большое множество разновидностей катушек индуктивности, отличающихся конфигурацией и областью применения. Ниже предоставлено ряд формул, показывающих, как найти индуктивность катушки:

1. Измерение индуктивности стандартной катушки производится по формуле:

• L – характеристика катушки (Гн);
• µ0 – магнитная const;
• µ – проницаемость вещества сердечника;
• N – количество оборотов проводника;
• S – площадь диаметрального разреза (м2);
• l – активная часть катушки в метрах.

1. Индуктивность прямого проводника:

• L – характеристика катушки (нГн);
• l – размер проводника;
• d – диаметр провода.

1. Определять индуктивности катушек с воздушным сердечником возможно благодаря формуле:

• L – характеристика катушки (мкГн);
• r – наружный радиус;
• l – активная часть катушки.

1. Индуктивность многослойной катушки с воздушным сердечником:

• L – характеристика катушки (мкГн);
• r – усредненный радиус катушки;
• l – активная часть катушки;
• d – глубина катушки.

1. Индуктивность плоской катушки:

• L – характеристика катушки (мкГн);
• r – усредненный радиус катушки;
• d – глубина катушки.

В радиотехнике часто используется сопряжение нескольких катушек. При последовательном или параллельном соединении катушек индуктивности используются различные формулы, находящие общую индуктивность.

Суммарная индуктивность, при последовательном подсоединении, рассчитывается как:

При параллельном соединении катушек суммарная индуктивность равна выражению:

Примеры использования на практике

Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.

Работает этот важный узел следующим образом:

1. На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
2. Электрическая цепь резко обрывается специальным прерывателем.
3. Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
4. Искровой разряд зажигает топливную смесь, приводя в движение поршень.

В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.

Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.

В блоках питания электронной аппаратуры таким же способом убирают:

• шумы:
• пульсации;
• нежелательные частоты.

Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.

Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.

В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.

В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.