Техническая механика

Основные понятия об изгибе

Деформация изгиба характеризуется потерей прямолинейности или первоначальной формы линией балки (ее осью) при приложении внешней нагрузки. При этом, в отличие от деформации сдвига, линия балки изменяет свою форму плавно.
Легко убедиться, что на сопротивляемость изгибу влияет не только площадь поперечного сечения балки (бруса, стержня и т. д.), но и геометрическая форма этого сечения.

Поскольку изгиб тела (балки, бруса и т. п.) осуществляется относительно какой-либо оси, на сопротивляемость изгибу влияет величина осевого момента инерции сечения тела относительно этой оси.
Для сравнения — при деформации кручения сечение тела подвергается закручиванию относительно полюса (точки), поэтому на сопротивление кручению оказывает влияние полярный момент инерции этого сечения.

На изгиб могут работать многие элементы конструкций – оси, валы, балки, зубья зубчатых колес, рычаги, тяги и т. д.

В сопротивлении материалов рассматривают несколько типов изгибов:
— в зависимости от характера внешней нагрузки, приложенной к брусу, различают чистый изгиб и поперечный изгиб;
— в зависимости от расположения плоскости действия изгибающей нагрузки относительно оси бруса — прямой изгиб и косой изгиб.

Чистый и поперечный изгиб балки

Чистым изгибом называется такой вид деформации, при котором в любом поперечном сечении бруса возникает только изгибающий момент (рис. 2).
Деформация чистого изгиба будет, например, иметь место, если к прямому брусу в плоскости, проходящей через ось, приложить две равные по величине и противоположные по знаку пары сил. Тогда в каждом сечении бруса будут действовать только изгибающие моменты.

Если же изгиб имеет место в результате приложения к брусу поперечной силы (рис. 3), то такой изгиб называется поперечным . В этом случае в каждом сечении бруса действует и поперечная сила, и изгибающий момент (кроме сечения, к которому приложена внешняя нагрузка).

Если брус имеет хоть одну ось симметрии, и плоскость действия нагрузок совпадает с ней, то имеет место прямой изгиб , если же это условие не выполняется, то имеет место косой изгиб .

При изучении деформации изгиба будем мысленно представлять себе, что балка (брус) состоит из бесчисленного количества продольных, параллельных оси волокон.
Чтобы наглядно представить деформацию прямого изгиба, проведем опыт с резиновым брусом, на котором нанесена сетка продольных и поперечных линий.
Подвергнув такой брус прямому изгибу, можно заметить, что (рис. 1):

— поперечные линии останутся при деформации прямыми, но повернутся под углом друг другу;
— сечения бруса расширятся в поперечном направлении на вогнутой стороне и сузятся на выпуклой стороне;
— продольные прямые линии искривятся.

Из этого опыта можно сделать вывод, что:

— при чистом изгибе справедлива гипотеза плоских сечений;
— волокна, лежащие на выпуклой стороне растягиваются, на вогнутой стороне – сжимаются, а на границе между ними лежит нейтральный слой волокон, которые только искривляются, не изменяя своей длины.

Полагая справедливой гипотезу о не надавливании волокон, можно утверждать, что при чистом изгибе в поперечном сечении бруса возникают только нормальные напряжения растяжения и сжатия, неравномерно распределенные по сечению.
Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной осью . Очевидно, что на нейтральной оси нормальные напряжения равны нулю.

Изгибающий момент и поперечная сила

Как известно из теоретической механики, опорные реакции балок определяют, составляя и решая уравнения равновесия статики для всей балки. При решении задач сопротивления материалов, и определении внутренних силовых факторов в брусьях, мы учитывали реакции связей наравне с внешними нагрузками, действующими на брусья.
Для определения внутренних силовых факторов применим метод сечений, причем изображать балку будем только одной линией – осью, к которой приложены активные и реактивные силы (нагрузки и реакции связей).

Рассмотрим два случая:

1. К балке приложены две равные и противоположные по знаку пары сил.
Рассматривая равновесие части балки, расположенной слева или справа от сечения 1-1 (рис. 2), видим, что во всех поперечных сечениях возникает только изгибающий момент М_и , равный внешнему моменту. Таким образом, это случай чистого изгиба.

Изгибающий момент есть результирующий момент относительно нейтральной оси внутренних нормальных сил, действующих в поперечном сечении балки.

Обратим внимание на то, что изгибающий момент имеет разное направление для левой и правой частей балки. Это говорит о непригодности правила знаков статики при определении знака изгибающего момента.

2. К балке приложены активные и реактивные силы (нагрузки и реакции связей), перпендикулярные оси (рис. 3). Рассматривая равновесие частей балки, расположенных слева и справа, видим, что в поперечных сечениях должны действовать изгибающий момент М _и и поперечная сила Q .
Из этого следует, что в рассматриваемом случае в точках поперечных сечений действуют не только нормальные напряжения, соответствующие изгибающему моменту, но и касательные, соответствующие поперечной силе.

Поперечная сила есть равнодействующая внутренних касательных сил в поперечном сечении балки.

Обратим внимание на то, что поперечная сила имеет противоположное направление для левой и правой частей балки, что говорит о непригодности правила знаков статики при определении знака поперечной силы.

Изгиб, при котором в поперечном сечении балки действуют изгибающий момент и поперечная сила, называется поперечным .

У балки, находящейся в равновесии вод действием плоской системы сил, алгебраическая сумма моментов всех активных и реактивных сил относительно любой точки равна нулю; следовательно, сумма моментов внешних сил, действующих на балку левее сечения, численно равна сумме моментов всех внешних сил, действующих на балку правее сечения.
Таким образом, изгибающий момент в сечении балки численно равен алгебраической сумме моментов относительно центра тяжести сечения всех внешних сил, действующих на балку справа или слева от сечения .

У балки, находящейся в равновесии под действием плоской системы сил, перпендикулярных оси (т. е. системы параллельных сил), алгебраическая сумма всех внешних сил равна нулю; следовательно сумма внешних сил, действующих на балку левее сечения, численно равна алгебраической сумме сил, действующих на балку правее сечения.
Таким образом, поперечная сила в сечении балки численно равна алгебраической сумме всех внешних сил, действующих справа или слева от сечения .

Так как правила знаков статики неприемлемы для установления знаков изгибающего момента и поперечной силы, установим для них другие правила знаков, а именно: Если внешняя нагрузка стремится изогнуть балку выпуклостью вниз, то изгибающий момент в сечении считается положительным, и наоборот, если внешняя нагрузка стремится изогнуть балку выпуклостью вверх, то изгибающий момент в сечении считается отрицательным (рис 4,a).

Если сумма внешних сил, лежащих по левую сторону от сечения, дает равнодействующую, направленную вверх, то поперечная сила в сечении считается положительной, если равнодействующая направлена вниз, то поперечная сила в сечении считается отрицательной; для части балки, расположенной справа от сечения, знаки поперечной силы будут противоположными (рис. 4,b). Пользуясь этими правилами, следует мысленно представлять себе сечение балки жестко защемлённым, а связи отброшенными и замененными реакциями.

Еще раз отметим, что для определения реакций связей пользуются правилами знаков статики, а для определения знаков изгибающего момента и поперечной силы – правилами знаков сопротивления материалов.
Правило знаков для изгибающих моментов иногда называют «правилом дождя» , имея в виду, что в случае выпуклости вниз образуется воронка, в которой задерживается дождевая вода (знак положительный), и наоборот – если под действием нагрузок балка выгибается дугой вверх, вода на ней не задерживается (знак изгибающих моментов отрицательный).

Виды деформации

Различают деформации нескольких видов. На изображении показаны некоторые из них.

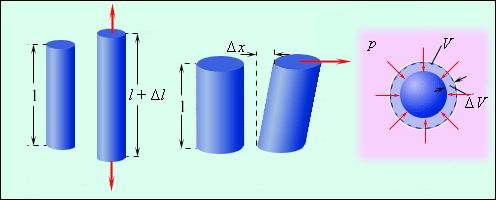
Рисунок 3 . 7 . 1 . Некоторые виды деформаций твердых тел: 1 – деформация растяжения; 2 – деформация сдвига; 3 – деформация всестороннего сжатия.

Первый вид – растяжение или сжатие – является наиболее простым видом деформации. В таком случае изменения, происходящие с телом, можно описать при помощи абсолютного удлинения Δ l , которое происходит под действием сил, обозначаемых F → . Взаимосвязь, существующая между силами и удлинением, обусловлена геометрическими размерами тела (в первую очередь толщиной и длиной), а также механическими свойствами вещества.

Если мы разделим величину абсолютного удлинения на первоначальную длину твердого тела, мы получим величину его относительного удлинения (относительной деформации).

Обозначим этот показатель ε и запишем следующую формулу:

Относительная деформация тела растет при его растяжении и соответственно уменьшается при сжатии.

Если учесть, в каком именно направлении внешняя сила действует на тело, то мы можем записать, что F будет больше нуля при растяжении и меньше нуля при сжатии.

Деформация изгиба

Рассмотрим примеры деформации данного вида. В случае изгиба, выпуклая часть тела подвергается некоторому растяжению, а вогнутый фрагмент сжимается. Внутри тела, подвергающегося данному варианту деформации, есть слой, который не испытывает ни сжатия, ни растяжения. Его принято называть нейтральным участком деформируемого тела. Вблизи него можно уменьшить площадь тела.

В технике примеры деформации данного типа используют для экономии материалов, а также для уменьшения веса возводимых конструкций. Сплошные брусья и стержни заменяют трубами, рельсами, двутавровыми балками.

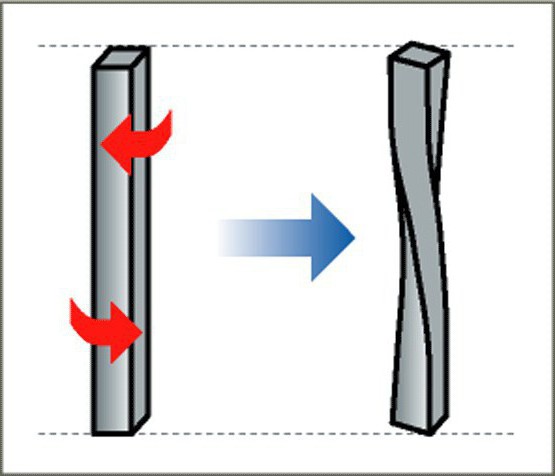
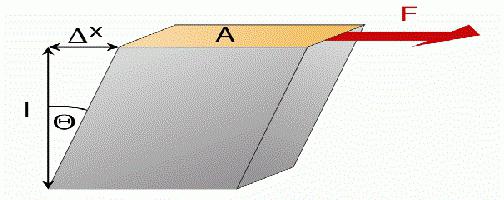
Сдвиг

Как уже было сказано, существуют различные виды деформации. Они подразделяются по характеру изменения формы тела. В механике сдвигом называют такое изменение формы, при котором нижняя часть бруса закреплена неподвижно, а сила прикладывается касательно к верхней поверхности. Относительная деформация сдвига определяется по следующей формуле:

где Х₁₂ — это абсолютный сдвиг слоёв тела (то есть расстояние, на которое сместился слой); В — это расстояние между закреплённым основанием и параллельным сдвинутым слоем.

Расчет в Excel коэффициента деформационного упрочнения.

При изгибе пластины из металла возникает упругопластическая деформация – наружные слои металла растягиваются, а внутренние (ближние к центру радиуса) сжимаются. Области сечения, подвергающиеся пластической деформации, упрочняются. При этом металл теряет вязкость и пластичность неравномерно по сечению. Сильнее происходит упрочнение слоёв, расположенных ближе к внешним поверхностям. Напряжения в области сечения вблизи нейтральной линии в зависимости от отношения радиуса изгиба к толщине металла могут и не достичь предела текучести, эта область может остаться в зоне упругих, то есть обратимых деформаций. Тем не менее, можно, сделав определенные допущения, предположить, что в процессе гибки происходит общее упрочение металла сечения в зоне изгиба – возрастает «средний» предел текучести.

Вывод формулы:

1. Формула классического сопромата для изгибающего момента листа (прямоугольного сечения)

M = K * [ σ_т ] * W_x = K * [ σ_т ] * b * s 2 /6

2. Формула для изгибающего момента с константами кривой деформационного упрочнения

M = A * b * s 2 /(2 m +1 *(2+ m )* r_г m )

3. Приравняв правые части формул друг другу, выразим коэффициент повышения предела текучести металла

K =3* A /(2 m *(2+ m )* r_г m * [ σ_т ] )

Из полученного выражения очевидно, что коэффициент упрочнения зависит от механических свойств металла и относительного радиуса изгиба детали.

Коэффициент деформационного упрочнения металла показывает во сколько раз возрастает предел текучести металла при изгибе.

Программа в MS Excel:

В качестве исходных данных для примера взяты механические свойства стали С345 (сталь 09Г2С). Листовая заготовка толщиной 20 мм гнется с внутренним радиусом 40 мм.

Использованные в программе формулы:

7. ε_т = [σ_т] / E +0,002

8. m =lg ( [σ_в] / [σ_т] )/lg ( ε_в / ε_т )

9. A = [σ_в] /( g * ε_в m )= [σ_т] /(g* ε_т m )

10. n = A *2 (2,59- m ) /( E /g*(2+ m ))

11. R _о = s /ln (1+ s / R )≈ R + s /2

12. r _о = R_о / s

13. R _г = R_о /(1+ n * r_о (1- m ) )

14. r _г = R_г / s

15. K =3* A /(2 m *(2+ m )* r _г m * [ σ_т ] /g)

График зависимости упрочнения металла от относительного радиуса изгиба:

Как следует из графика в рассмотренном примере деформационное упрочнение металла максимально при минимальном радиусе гибки: K ( r_г =1)=2,24. Если обратиться к статье «Расчет усилия листогиба», то увидим, что произведение использованных там поправочных коэффициентов запаса и упрочнения: k 1 * k 2 =1,25*1,8=2,25. Весьма близкие значения…

Все полученные выше результаты являются простой математической связкой теории сопромата и эмпирической теории степенной зависимости напряжений от деформаций.

Возможно, предложенный в статье взгляд на тему покажется специалистам слишком неточным примитивным и устаревшим. Более того, я не исключаю, что представленные результаты могут быть ошибочными, особенно в области r_г Уважающих труд автора прошу скачивать файл с программой после подписки на анонсы статей в окне, размещенном в конце статьи или в окне наверху страницы!

Деформация твёрдого тела может явиться следствием фазовых превращений, связанных с изменением объёма, теплового расширения, намагничивания (магнитострикция), появления электрического заряда (пьезоэлектрический эффект) или же результатом действия внешних сил.

Деформация называется упругой, если она исчезает после удаления вызвавшей её нагрузки (то есть тело возвращается к первоначальным размерам и форме), и пластической, если после снятия нагрузки деформация не исчезает (или исчезает не полностью).

Все реальные твёрдые тела при деформации в большей или меньшей мере обладают пластическими свойствами. При некоторых условиях пластическими свойствами тел можно пренебречь, как это и делается в теории упругости. Твёрдое тело с достаточной точностью можно считать упругим, то есть не обнаруживающим заметных пластических деформаций, пока нагрузка не превысит некоторого предела (предел упругости).

Природа пластической деформации может быть различной в зависимости от температуры, продолжительности действия нагрузки или скорости деформации. При неизменной нагрузке, приложенной к телу, деформация изменяется со временем; это явление называется ползучестью. С возрастанием температуры скорость ползучести увеличивается. Частными случаями ползучести являются релаксация и упругое последействие. Одной из теорий, объясняющих механизм пластической деформации, является теория дислокаций в кристаллах.

Перемещение — изменение положения точки тела в пространстве вследствие изменения его формы и размеров под действием нагрузки. Полное перемещение точки в пространстве раскладывается на компоненты u, v и w, параллельные осям x, y и z, соответственно.

Деформация — изменение формы и размеров тела.

Перемещения рассматриваемой точки зависит от деформации всех нагруженных областей тела и включают также в себя перемещения как жесткого целого ненагруженных областей. Поэтому перемещения не могут характеризовать степень деформирования в окрестности рассматриваемой точки. Для этого используют понятие деформации. В отдельных случаях их величины могут совпадать (растяжение стержня), но в общем случае — это разные вещи.

Остановимся еще на одном важном моменте. Очень часто путают два понятия — «деформация» и «перемещение» — хотя ясно, что они не адекватны. Например, представим себе канат, прикрепленный к потолку. По канату на некоторую высоту поднялся человек. Очевидно, что под действием веса человека (пренебрегая весом каната) деформируется (растягивается) только верхняя часть каната, заключенная между потолком и местом, где находится человек. Нижняя часть каната не деформируется, а перемещается как твердое тело. Следовательно, не всегда перемещения сечений какого-то участка стержня непосредственно связаны с его деформацией.

Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. 3-е изд. — М.: Высшая школа, 2003.

Деформации могут быть угловые и линейные.

Линейная деформация характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.

Угловая деформация характеризует изменение формы тела и чаще всего называется углом сдвига.

Угол сдвига — это изменение первоначально прямого угла. γ = α + β .

Полная деформация — это сумма линейной и угловой деформации.

Если взять малый элемент тела параллелепипед, ориентированный по осям x, y, z, то соответственно возникает три линейных деформации (вдоль осей x, y, z ) ε_x,ε_y, ε_z
$epsilon _x = <�Δdxover dx>, quad epsilon _y = <�Δdyover dy>,quad epsilon _z = <�Δdzover dz>$
и три угловые деформации [math]gamma _, gamma _, gamma _[/math] в трех взаимно-перпендикулярных плоскостях.

Относительные линейные и угловые деформации – величины безразмерные.

Деформации упругие и пластические

Деформации делятся на упругие и пластические (остаточные).

• Упругими деформациями называются деформации, исчезающие после снятия вызвавших их сил.
• Пластичными деформациями называются деформации, не исчезающие после снятия вызвавших их сил.

Типы деформаций

В зависимости от приложенных к телу нагрузок различают несколько видов деформации, отличающиеся законом распределения напряжений по сечению тела.

Растяжение-сжатие в поперечном сечении действует только одно внутреннее усилие, не равное нулю — продольное усилие. Конструкция В этом случае говорят о линейной деформации конструкции (характеризуется абсолютным и относительным удлинением, остальными деформациями пренебрегают). Чистый сдвиг в поперечном сечении действует только поперечная сила. В этом случае линейные относительные деформации равны нулю, углы сдвига не равны нулю (характеризуется изменением формы) Кручение в поперечном сечении действует только крутящий момент. Линейные относительные деформации равны нулю, углы сдвига не равны нулю. Изгиб в поперечном сечении действуют изгибающий момент и поперечная сила. Сложное сопротивление одновременное действие нескольких типов простых деформаций — растяжения-сжатия, кручения, изгиба.

Для каждого из указанных видов деформации существуют свои формулы для расчета на прочность.

Деформация растяжения

Деформация растяжения — вид деформации, при которой нагрузка прикладывается продольно от тела, то есть соосно или параллельно точкам крепления тела. Проще всего растяжение рассмотреть на буксировочном тросе для автомобилей. Трос имеет две точки крепления к буксиру и буксируемому объекту, по мере начала движения трос выпрямляется и начинает тянуть буксируемый объект. В натянутом состоянии трос подвергается деформации растяжения, если нагрузка меньше предельных значений, которые может он выдержать, то после снятия нагрузки трос восстановит свою форму.

Схема растяжения образца

Посмотрите прибор измеряющий деформацию растяжения →

Деформация растяжения является одним из основных лабораторных исследований физических свойств материалов. В ходе приложения растягивающих напряжений определяются величины, при которых материал способен:

1. воспринимать нагрузки с дальнейшим восстановлением первоначального состояния (упругая деформация)
2. воспринимать нагрузки без восстановления первоначального состояния (пластическая деформация)
3. разрушаться на пределе прочности

Данные испытания являются главными для всех тросов и веревок, которые используются для строповки, крепления грузов, альпинизма. Растяжение имеет значение также при строительстве сложных подвесных систем со свободными рабочими элементами.

Деформация сжатия

Деформация сжатия — вид деформации, аналогичный растяжению, с одним отличием в способе приложения нагрузки, ее прикладывают соосно, но по направлению к телу. Сдавливание объекта с двух сторон приводит к уменьшению его длины и одновременному упрочнению, приложение больших нагрузок образовывает в теле материала утолщения типа «бочка».

Схема сжатия образца

В качестве примера можно привести тот же прибор что и в деформации растяжения немного выше.

Деформация сжатия широко используется в металлургических процессах ковки металла, в ходе процесса металл получает повышенную прочность и заваривает дефекты структуры. Сжатие также важно при строительстве зданий, все элементы конструкции фундамента, свай и стен испытывают давящие нагрузки. Правильный расчет несущих конструкций здания позволяет сократить расход материалов без потери прочности.

Деформация сдвига

Деформация сдвига — вид деформации, при котором нагрузка прикладывается параллельно основанию тела. В ходе деформации сдвига одна плоскость тела смещается в пространстве относительно другой. На предельные нагрузки сдвига испытываются все крепежные элементы — болты, шурупы, гвозди. Простейший пример деформации сдвига – расшатанный стул, где за основание можно принять пол, а за плоскость приложения нагрузки – сидение.

Схема сдвига образца

Посмотрите прибор измеряющий деформацию сдвига →

Деформация изгиба

Деформация изгиба — вид деформации, при котором нарушается прямолинейность главной оси тела. Деформации изгиба испытывают все тела подвешенные на одной или нескольких опорах. Каждый материал способен воспринимать определенный уровень нагрузки, твердые тела в большинстве случаев способны выдерживать не только свой вес, но и заданную нагрузку. В зависимости от способа приложения нагрузки при изгибе различают чистый и косой изгиб.

Схема изгиба образца

Посмотрите прибор измеряющий деформацию изгиба →

Значение деформации изгиба важно для проектирования упругих тел, таких, как мост с опорами, гимнастический брус, турник, ось автомобиля и другие.

Деформация кручения

Деформация кручения – вид деформации, при котором к телу приложен крутящий момент, вызванный парой сил, действующих в перпендикулярной плоскости оси тела. На кручение работают валы машин, шнеки буровых установок и пружины.

Схема кручения образца

Посмотрите прибор измеряющий деформацию кручения →

Деформация изгиба

Деформации печатных плат могут возникать по ряду причин, в частности из-за:

• несоответствия исходных материалов требованиям производителей печатных плат
• воздействия высоких температур и влажности на этапе производства
• ошибок проектирования печатной платы
• следования разным стандартам качества: ГОСТ и IPC

В соответствии с принятым стандартом IPC-A-600 (Acceptability of printed boards — Критерии приемки печатных плат) качество плоскости печатной платы определяется двумя основными характеристиками: изгибом (bow) и скручиванием (twist).

Деформация изгиба. Стандарт IPC-T-50G (Terms and Definitions for Interconnecting and Packaging Electronic Circuits) определяет изгиб как отклонение от плоскости печатной платы, характеризующееся близкой к цилиндрической или сферической форме кривизной при условии, что все четыре угла печатной платы лежат в одной плоскости.

Деформация скручивания. Согласно ГОСТ 20406-75, скручивание – это деформация, характеризующаяся спиральным искривлением противоположных кромок основания печатной платы. При скручивании один угол платы находится не в той плоскости, в которой лежат остальные три угла.

Требования ГОСТ и IPC к деформации поверхности ПП

Согласно ГОСТ 23752-79, деформация при изгибе и скручивании печатных плат с жестким основанием на 100 мм длины не должна превышать значений, указанных в таблице. При использовании диэлектрика высшей категории качества деформация не должна превышать 0,4 мм, а в зоне концевых контактов — быть более 0,5 мм (для МПП – 0,4 мм). Отклонение от перпендикулярности сторон прямоугольной ПП при деформации скручивания не должно быть более 0,2 мм на 100 мм. Значения деформации для ПП толщиной 1,0 мм и менее не устанавливаются.

По IPC-A-600G, для печатных плат с поверхностно монтируемыми компонентами (SMD монтаж печатных плат) деформации при изгибе и скручивании ПП не должны превышать 0,75%. Для всех остальных — 1,5%, независимо от толщины печатной платы.

Как предотвратить деформации печатной платы на стадии производства и сборки

• следует выбирать базовые материалы для бессвинцовых сборок и избегать критического термического воздействия
• применять указанные параметры прессования для слоев платы
• не комбинировать материалы разных производителей в разных слоях
• использовать горизонтальные печи для отверждения

Как предотвратить деформации на стадии проектирования ПП

Существуют приемы, с помощью которых еще на стадии проектирования печатной платы можно если не устранить, то, по меньшей мере, существенно уменьшить величины возможных деформаций.

Баланс меди

Этот метод предусматривает заполнение свободных от меди областей на печатной плате медной фольгой. Если проводящий рисунок неравномерный, толщина слоя меди в готовой продукции будет различной в различных областях печатной платы, что может привести к деформации печатных плат. Чтобы снизить риск деформации, рисунок должен быть равномерным по каждому слою. Для многослойной печатной платы, насколько возможно, сигнальные слои и слои питания располагайте симметрично относительно центра платы. Выбирайте симметричные надстройки ядра, толщины препрегов и меди.

Изменить и улучшить дизайн печатных плат на стадии разработки нетрудно. В любой системе проектирования предусмотрены стандартные возможности для такой операции. Плата с хорошим балансом меди по всей поверхности существенно снижает величину деформаций. Правда для СВЧ плат эта рекомендация не очень подходит, для них не всегда возможно обеспечить строгий баланс меди.

Иммерсионные покрытия

Для печатных плат, толщиной 0,8 мм и менее, лучше всего использовать иммерсионные покрытия, такие, как, ENIG – Electroless Nickel/Immersion Gold – иммерсионное золото по подслою никеля или IS – Immersion Silver – иммерсионное серебро и др. Применение «стандартного» горячего лужения (HAL или HASL – Hot Air (Solder) Leveling) увеличивает вероятность появления деформации.

Симметричная структура для МПП

Для многослойных печатных плат оптимальна симметричная структура. В абсолютно симметричной структуре центром является препрег, относительно него симметрично располагаются одинаковые фольгированные диэлектрики, препреги и медная фольга внешних слоев. Величина изгиба и скручивания печатной платы с такой структурой будет в пределах стандартов.