Техническое черчение

Основы черчения

Строительное

Машиностроительное

Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).

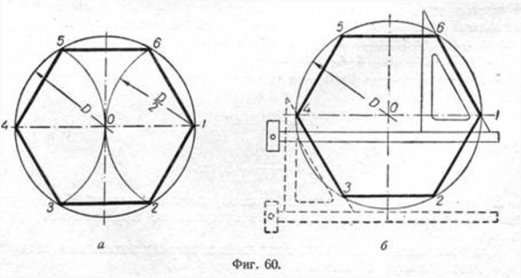
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.

Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.

Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны

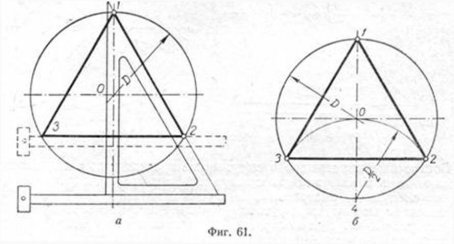
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

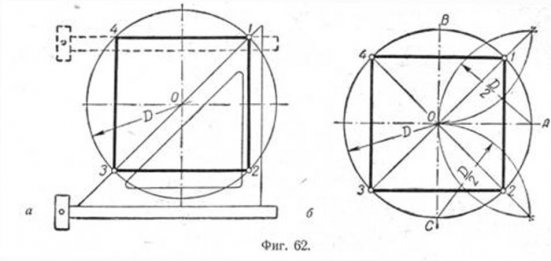
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.

Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.

Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

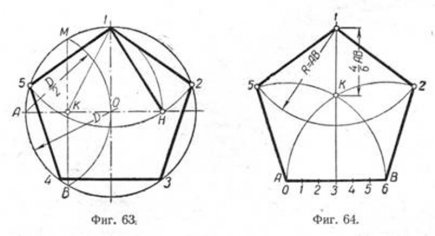
Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.

Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.

Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

Построение вписанного в окружность правильного семиугольника.

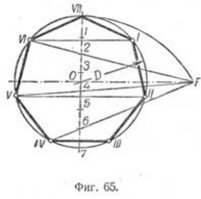Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

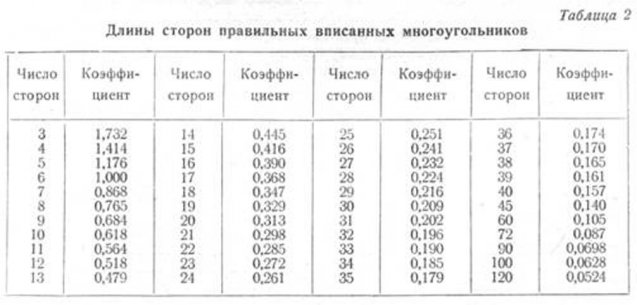
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты.

Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Точное построение фигуры

Специалисты рекомендуют некоторую последовательность действий, по которым построить правильный пятиугольник очень просто. Для операции необходимы обыкновенная тетрадь в клеточку, циркуль, карандаш, резинка и линейка. Следует выполнить некоторые шаги:

Построить окружность с центром в некоторой точке О.
Провести два диаметра. Они должны пересекаться под прямым углом.
Поставить точку V (пересечение окружности с одним из диаметров), которая является вершиной фигуры.
По левой стороне поставить точку D. Это пересечение диаметра (оси симметрии) с окружностью.
Отметить на отрезке OD точку А, которая делит его пополам.
Выполнить построение вспомогательной окружности, центром которой является точка, полученная в 5 пункте. Кроме того, круг с радиусом CV должен проходить через V.
Точку, полученную при пересечении диаметра и окружности, нужно обозначить литерой B.
Нарисовать окружность с радиусом, равным CV, из точки V.
Отметить пересечение круга с первой окружностью, центром которой является точка О. Искомое место пересечения обозначить литерой F (вторая вершина пентагона).
Поставить иглу циркуля в точку F и провести окружность через Е.
Обозначить пересечение окружностей с центрами в F и O точкой G, которая будет вершиной пентагона.
Аналогичным образом проделать шаг 11, только центр выбрать не в F, а в G. Полученную точку следует обозначить литерой H (последняя вершина фигуры).
Соединить пять точек (СVEFG) между собой с помощью линейки.

Читайте также Краска для вагонки

Если все пункты алгоритма выполнены правильно, то должен получиться пентагон, изображенный на рисунке 1:

Этот способ следует применять для точных построений и чертежей деталей. Однако для решения задач, в которых необходимо схематически изобразить пятиугольник, этот вариант не подойдет.

Правильный многоугольник:

Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.

Рис. 3. Правильный пятиугольник

Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников .

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.

Правильный 5 угольник как нарисовать

Первый способ — по данной стороне S с помощью транспортира.

Проводим прямую и откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.

Полученный пятиугольник — искомый.

Первый способ построения пятиугольника

Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е.

Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.

Второй способ построения пятиугольника

Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N₁, Р₁, Q₁, К₁ и соединяем их прямыми.

Третий способ построения пятиугольника

На рисунке построен шестиугольник по данной стороне.

Построение шестиугольника

Прямой АВ = 5, как радиусом, из точек А и В описываем дуги, которые пересекутся в С; из этой точки тем же радиусом описываем окружность, на которой сторона А В отложится 6 раз.

Шестиугольник ADEFGB — искомый.

«Отделка комнат при ремонте»,
Н.П.Краснов

Основанием для нанесения росписи служат полностью законченные окраской поверхности стен, потолков и других конструкций; роспись делается по высококачественным клеевым и масляным окраскам, сделанным под торцовку или флейц. Приступая к разработке эскиза отделки, мастер должен ясно представить себе всю композицию в бытовой обстановке и отчетливо осознать творческий замысел. Только при соблюдении этого основного условия можно правильно…

Обмер выполненных работ, за исключением особо оговоренных случаев, производится по площади действительно обработанной поверхности с учетом ее рельефа и за вычетом необработанных мест. Для определения действительно обработанных поверхностей при малярных работах следует пользоваться переводными коэффициентами, приведенными в таблицах. А. Деревянные оконные устройства (обмер производится по площади проемов по наружному обводу коробок) Наименование устройств Коэффициент при…

Мы уже говорили, что для исполнения некоторых видов малярных работ необходимо уметь рисовать. А умение рисовать, в свою очередь, предполагает знание правил построения геометрических фигур. Эскизы на бумаге вычерчивают при помощи треугольников, рейсшин, транспортаpa и циркуля, а на плоскости стен и потолков построения выполняются при помощи веска, линейки, деревянного циркуля и шнура. При этом надо…

Прямой угол, т. е. равный 90°, образуется двумя взаимно перпендикулярными линиями. Перпендикуляр строится следующим образом. Опустить перпендикуляр. Из данной точки С (лежащей вне прямой), как из центра, произвольным радиусом описываем дугу так, чтобы она пересекла данную прямую в двух точках D и Е из этих точек, как из центров, одинаковыми радиусами описываем дуги, чтобы они…

Построение угла, равного данному Угол, равный данному, строится следующим образом. Из вершины А данного угла произвольным радиусом проводим дугу тем же радиусом из точки D на данной прямой описываем дугу EF; величину дуги ВС откладываем по дуге EF до точки F и проводим DE. Угол EDF — искомый. Построение угла, равного данному Параллельные линии Линии,…

Способ построения правильного пятиугольника с помощью циркуль и линейку:

Рисуем окружность (зелёная) , такую чтобы длина стороны пятиугольника была

2,5 см. Затем проводим два перпендикулярных диаметра, отмечаем середину (точка C) одного из радиусов (OB), которая будет является центром новой окружности (розовая) с радиусом AC. Находим точку пересечения (D) этой окружности с диаметром. Строим новую окружность (синюю) с центром в точке A и радиусом AD. Точки пересечения с зелёной окружностью и будут углами пятиугольника. Из полученных точек (E и F) опять откладываем радиус и получаем точки (G и H), осталось только объединить полученные точки ( A E G H F).

Последние события

Найди отличия у картинок

Найди отличия в картинках. Игра на развитие внимательности. Проведите турнир. кто быстрее найдет все отличия на картинках.

Как нарисовать краба

На сегодняшнем уроке нарисуем краба по шагам. Это не сложно. Получится у всех.

Как нарисовать велосипед

Встречайте небольшой урок рисования. Рисуем велосипед по шагам.

Новые раскраски на 8 марта

Скоро замечательный весенний праздник — день женщин — 8 марта. Пора подумать об открытках. А так как лучшая открытка — это та, которая нарисована или сделана собственными руками, предлагаем скачать несколько раскрасок на тему 8 марта.

Открытки-раскраски на 8 марта

Почти все дети любят раскрашивать веселые картинки. предлагаем вам скачать, распечатать и раскрасить вместе с детьми забавные открытки-поздравления для мамы на 8 марта.

Трафареты печатных букв

Маленького ребенка можно научить писать печатные буквы с помощью трафаретов

Как из картинки сделать раскраску?

Раскраски любят и дети, и взрослые. И это неудивительно. Ведь даже не умея профессионально рисовать, можно создавать красивые рисунки, вкладывая в них своё умение и виденье .

Популярное

Архив

Как нарисовать правильную звездочку? Как нарисовать правильный пятиугольник? Как разделить круг на пять равных частей? На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной эти шаги.

Как нарисовать правильную звездочку?

Как нарисовать правильный пятиугольник?

Как разделить круг на пять равных частей?

На все эти вопросы вы сможете найти ответ, если проделаете вслед за мной вот эти шаги.

Конечно же, нам понадобится циркуль с карандашом и линейка.

Для начала нарисуйте циркулем круг.

Разделите его на четыре части линиями сверху вниз и справа налево.

Читайте также Водяные редукторы давления

Можно сразу объяснить ребенку, что отрезок, соединяющий две точки на окружности и проходящий через ее центр, называется диаметр.

А отрезок, соединяющий центр и точку на окружности, называется радиус.

С помощью линейки измерьте и разделите пополам один из радиусов.

У меня это отрезок слева от центра.

Серединку радиуса я обозначила

Нам понадобится точка сверху окружности.

Ее я обозначила цифрой 0.

Устанавливаем иголку циркуля

в точку 1, а карандашик в точку 0.

Рисуем дугу до пересечения с горизонтальным диаметром.

Обозначаем точку пересечения

Сейчас устанавливаем иголку циркуля

в точку 0, а карандашик в точку 2.

И рисуем дугу до пересечения с окружностью, причем с двух сторон.

Точки пересечения помечены

Не меняя ширину циркуля, устанавливаем иголку

в точку 3 и отмеряем кусочек окружности.

Точку 6 можно отмерить и от

точки 5 и от точки 4.

Главное, не изменять ширину (раствор) ножек циркуля.

Вот, практически и все.

Если соединим точки, получим правильный пятиугольник.

Рисование звезды с помощью «Многоугольника» (Polygon Tool)

Чтобы нарисовать звезду при помощи этого инструмента, нажмите на значок шестеренки в панели параметров, а затем выберите опцию «Звезда» (Star):

Нажатие на значок шестеренки и выбор опции «Звезда» (Star).

Затем просто нажмите внутри документа и создайте фигуру звезды методом перетаскивания курсора. При активной опции «Звезда» (Star), опция «Стороны» (Sides) в панели параметров задаёт количество лучей звезды. Так, при его значении 5 у нас получится пятиконечная звезда:

Пятиконечная звезда, начерченная с помощью инструмента «Многоугольник», параметры фигуры заданы по умолчанию.(Polygon Tool).

Изменение значения сторон на 8 дает нам восьмиконечную звезду:

Управление количеством лучей звезды.

Мы можем изменять у звездообразной фигуры не только количество лучей, но и положение внутренних вершин между центром звезды и внешними вершинами. По умолчанию, внутренние вершины находятся посередине, за это отвечает параметр «Глубина лучей» (Indent Sides By), по умолчанию он равен 50%:

Изменение параметра «Глубина лучей» (Indent Sides By) с 50 процентов, заданных по умолчанию, до 90%.

Посмотрите, что получилось:

Та же восьмиконечная звезда, но со значением параметра «Глубина лучей» (Indent Sides By) 90%. Контур скрыт.

По умолчанию, звезды имеют острые углы на вершинах, но мы можем сделать их закруглёнными, выбрав опцию «Сгладить внешние углы» (Smooth Corners):

Включение скругления углов при помощи опции «Сгладить внешние углы» (Smooth Corners).

Во как будет выглядеть стандартная пятиконечная звезда со сглаженными вершинами лучей при включенной опции «Сгладить внешние углы» (Smooth Corners):

Опция сглаживания углов придает звезде веселый, дружелюбный вид.

Мы можем сгладить не только вершины лучей, но и вершины впадин с помощью опции «Сгладить внутренние углы» (Smooth Indents):

Включение опции «Сгладить внутренние углы» (Smooth Indents).

При включении обеих этих опций мы получаем форму, похожую на морскую звезду:

Звезда с сглаженными углами и впадинами получена при одновременном включении опций «Сгладить внешние углы» (Smooth Corners) и «Сгладить внутренние углы» (Smooth Indents).

Определение и построение

Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.

Если вспомнить формулу суммы углов многоугольника

то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.

Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.

Пошаговая инструкция будет выглядеть так:
1. чертится прямая линия и на ней ставится точка;
2. из этой точки строится окружность (она является ее центром);
3. из мест пересечения окружности с линией строятся еще две таких же, они должны сойтись в центре.
4. после этого отрезками последовательно соединяются все точки на первой окружности.
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.

Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.

Пятиугольник, пентаграмма, звезда…

Задача о построении правильных многоугольников очень стара, и в её рамках особое место занимает построение пятиугольника. Уже хотя бы потому, что он первый из всех таких фигур, который строится нетривиально. (Действительно, правильный — т.е. равносторонний — треугольник строится всего двумя засечками циркуля, а построение правильного четырёхугольника — квадрата — сводится всего лишь к двум перпендикулярным прямым.)

Греки решили этот вопрос: пятиугольнику посвящены предложения 10 и 11 четвёртой книги “Начал” Эвклида. В Средние века задача обрела новую актуальность, ибо пятиугольник являлся основой пентаграммы — важнейшего мистического символа. Ну, а в советские времена не менее важным символом считалась пятиконечная звезда, которая также строится на основе пятиугольника.

Рассмотрим три геометрических рецепта из разных времён.

Правильный пятиугольник Эвклида

Если выкладки из “Начал” (не факт, конечно, что именно Эвклид был их автором) изложить не в виде теорем, а в виде алгоритма, то получится следующее:
1. Построить окружность с центром в точке О. Произвольно отметить на ней точку А. Провести через точки О и А диаметр.
2. Провести второй диаметр перпендикулярно ОА. Точку его пересечения с окружностью (любую из двух) обозначить В.
3. Разделить отрезок ОВ пополам точкой С.
4. Провести окружность с центром в точке С через точку А. Точку её пересечения с прямой ОВ, лежащую внутри исходной окружности, обозначить D.
5. Провести окружность с центром в точке А и радиусом AD. Точки её пересечения с исходной окружностью обозначить Е и F.
Дуги AE=AF будут составлять пятую часть исходной окружности.

Этот способ довольно прост и даёт правильный пятиугольник. Как видно, основой построения в нём является вписывание в окружность.

Моноциркульный пятиугольник Дюрера

Относительно следующего построения долгое время считалось, что его нашёл великий художник и очень неплохой математик Альбрехт Дюрер: именно в его книге “Vnderweysung der messung mit dem zirckel vnd richtscheyt” (“Наставление в измерении циркулем и линейкой”, 1525) встречалось самое раннее известное упоминание. Сам Дюрер, впрочем, авторства себе не приписывал, а в конце XIX века был обнаружен анонимный трактат примерно 1484 года, ныне упоминаемый как “Geometria deutsch”. Он содержит описание того же построения, которое, таким образом, является более старым, нежели предполагалось. Возможно, его открытие принадлежит арабам, которые любили задачи с постоянным раствором циркуля.

Следующее описание приводится непосредственно по “geometria deutsch”.

Если кто хочет нарисовать пятиугольник с циркулем неизменного раствора, то раскрой циркуль настолько широко, сколько ты желаешь, и наметь [этим раствором] две точки А, В.

Затем оставь одно острие циркуля в точке А и проведи круг; точно так же оставь циркуль в точке В и проведи круг, и там, где один круг заходит за другой, наметь две точки С, D. Затем наложи линейку на точки С и D и проведи длинную черту через обе точки, так что получится такой чертёж:

Затем помести острие циркуля в точку D и проведи круг через А, В, и там, где этот круг проходит через черту CD, наметь E. Затем посмотри, где этот самый круг заходит за круг DBH [см. примечание!] и наметь там F, точно так же на другой стороне наметь G. После этого наложи линейку на точку F и на Е и проведи черту через эти точки до круга DACG и наметь там точку К. Таким же образом на другой стороне наметь Н. После этого помести циркуль в точку К и проведи круг, и где он заходит за линию DEC, наметь I. Затем проведи черту от I до К, от К до В, от В до А, от А до Н, от Н до I. Тогда ты получишь правильный пятиугольник, образец которого здесь приложен.

“Пятиугольник Дюрера” (“Fünfort”) является равносторонним, но в действительности не является правильным. Вместо 108° его углы составляют 107°2’13’’ (при вершинах А,В), 108°22’ (при вершинах Н,К) и 109°11’33’’ (при вершине I). Этот факт был установлен венецианским математиком Дж.Бенедетти в 1580 и позднее подтверждён Хр.Клавием в 1604 расчётом по другой методике.

ПРИМЕЧАНИЕ . В тексте упоминается точка Н до того, как она построена. Это, впрочем, является простым недоразумением, так как по описанию вполне понятно, что речь идёт о левой из двух начально построенных окружностей. Очевидно, автор сначала подготовил полный чертёж и затем уже по нему составлял описание.

Советская пятиугольная звезда

В книгах и журналах эпохи СССР было опубликовано много геометрических рецептов построения звезды; часто встречалось уже описанное построение Эвклида. Были и оригинальные методы — так, например, следующий алгоритм интересен тем, что изначально ориентирован на построение именно звезды (не пятиугольника) и, в отличие от эвклидовского, не требует предварительного проведения окружности, в которую впоследствии вписывается фигура.
1. Построить отрезок АВ и разделить его на восемь равных частей. (Это можно сделать, например, трёхкратным делением пополам, или просто восемь раз отложить промежуточную величину.) Этот отрезок впоследствии будет диагональю звезды.
2. Отметить на отрезке точки Е и G такие, что АЕ=GB и составляет 3/8 длины отрезка.
3. Провести окружности и . Точки их пересечения обозначить К и J.
4. Ломаная AEKGB образует часть контура звезды.
5. Провести окружности и .
6. Найти точки пересечения окружностей
  L = × и
  M = × ,
  ближайшие к точке J.
7. Ломаная LJM образует часть контура звезды.
8. Достроить контур звезды, пользуясь линиями LB, AM, KL, KM.
Звезда, построенная по этой методике, очень близка к правильной, но всё же не является ей. При внимательном рассмотрении увеличенного чертежа можно увидеть, что точка J не лежит на линиях LB и AM, точка Е не лежит на линии KL, а точка G не лежит на линии КМ.

Площадь фигуры

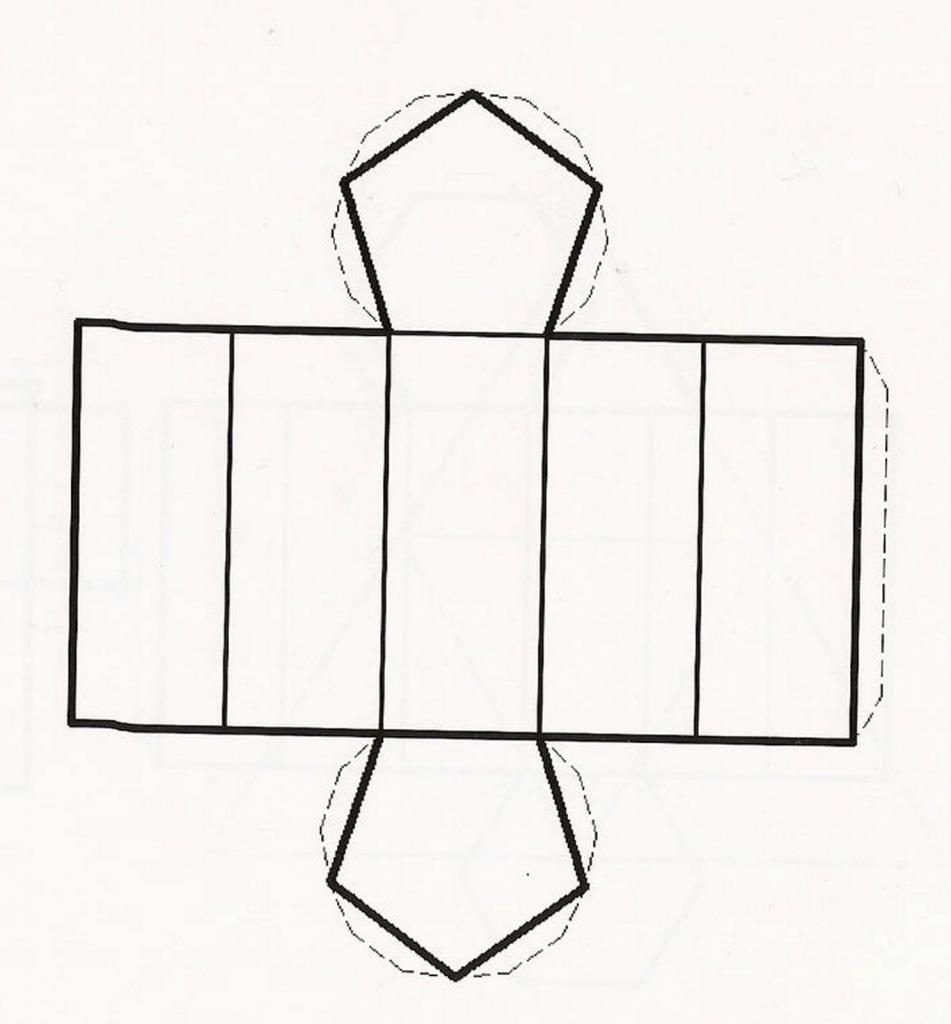
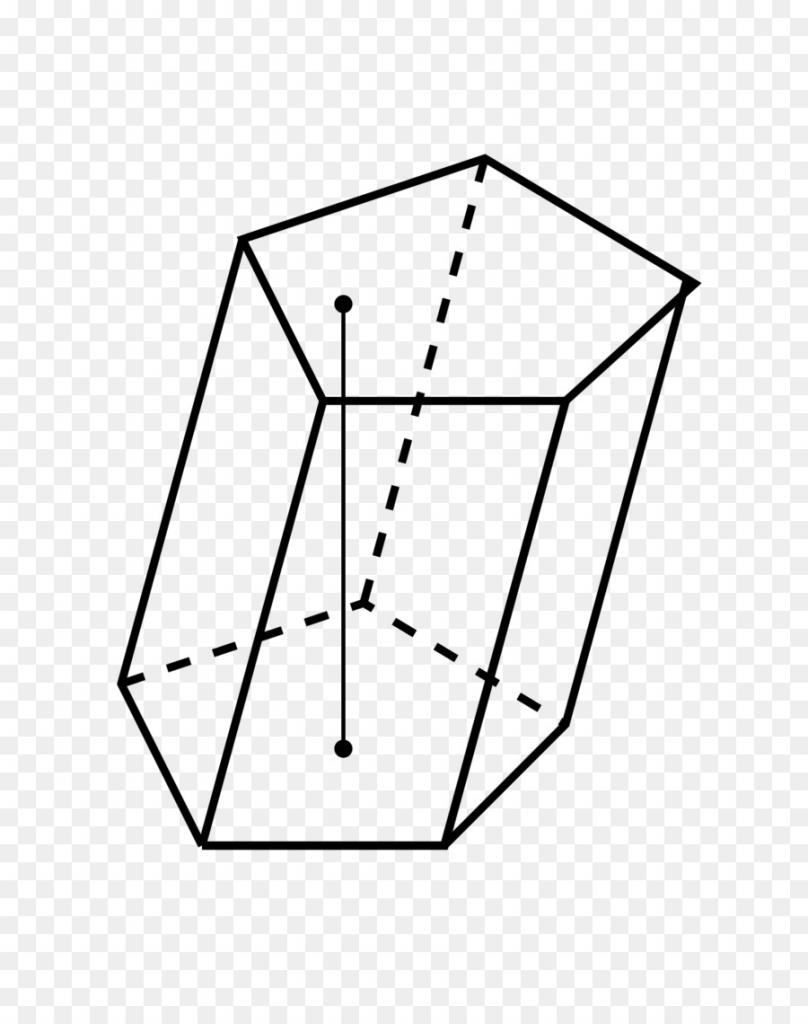
Теперь рассмотрим вопрос, как найти площадь пятиугольной призмы. На рисунке ниже приведена ее развертка. Видно, что искомая площадь образована двумя одинаковыми пятиугольниками и пятью равными друг другу прямоугольниками.

Площадь всей поверхности фигуры выразится формулой:

Здесь индексы o и p означают основание и прямоугольник соответственно. Обозначим длину стороны пятиугольника как a, а высоту фигуры как h. Тогда для прямоугольника запишем:

Чтобы вычислить площадь пятиугольника, воспользуемся универсальной формулой:

Где n — число сторон многоугольника. Подставляя n = 5, получаем:

Точность полученного равенства составляет 3 знака после запятой, что вполне достаточно для решения любых задач.

Теперь остается найти сумму полученных площадей основания и боковой поверхности. Имеем:

Следует помнить, что полученная формула справедлива только для прямоугольной призмы. В случае с косоугольной фигурой площадь ее боковой поверхности находят, исходя из знания периметра среза, который должен быть перпендикулярен всем параллелограммам.

Как правильно изобразить шестигранную призму?

Шестигранная призма строится уже значительно сложнее. Можно идти по принципу построения четырехгранной призмы, где сначала обозначается основа, а затем достраиваются боковые грани. Можно строить иначе. Для того, чтобы правильно построить шестигранную призму, мы должны построить четырехгранную.

При этом мы делим переднюю грань пополам, создавая дополнительные грани. Этот способ сложнее, так как ошибка на первом этапе может испортить итоговый результат. Шестигранную призму мы строим с применениями знаний о раскрытии эллипсов, что способствует правильному определению размеров граней. Как и любой предмет, объемность призмы создается с помощью светотени. Начинаем штриховку равномерно, после чего добираем тон в самых темных участках.
Читайте также: