Детали машин

Детали машин

Эвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие.

В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:

• w – начальной;
• b – основной;
• a – вершин зубьев;
• f – впадин зубьев.

Параметрам, относящимся к делительной окружности, индекс не присваивается.

При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» — колесу.

Начальные окружности

Начальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О₁ и О₂ до полюса П ) при неизменном межосевом расстоянии О₁О₂ тоже остается неизменным.
При изменении межосевого расстояния a_w меняются и диаметры d_w начальных окружностей шестерни и колеса, т. е. у пары зубчатых колес может быть множество начальных окружностей.
У отдельно взятого колеса начальной окружности не существует – по определению этот параметр образуется в зацеплении, т. е. в зубчатой передаче.

Межосевое расстояние определяется по формуле:

Делительная окружность

Окружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным.

Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей.

У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.:

Исключение составляют передачи с угловой модификацией.

Окружной шаг зубьев

Расстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1).
Для пары зацепляющихся зубчатых колес окружной шаг зубьев должен быть одинаковым.

Основной шаг

Этот параметр, обозначаемый p_b , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу p_b .
Из треугольника О₂ВП (см. рис. 1) диаметр основной окружности d_b2 = 2 r_b2 = d₂ cos α_w , откуда основной шаг может быть определен по формуле:

Окружная толщина зуба и окружная ширина впадины

Окружная толщина зуба s_t и окружная ширина впадины e_t по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер s_t назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда s_t + e_t = p .

Окружной модуль зубьев

Из определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно,

Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах:

d = mz или m = d/z .

Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб.

Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым.

Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм.
В соответствии со стандартным рядом I модуль может принимать следующие значения: 1,0, 1,25, 1,5, 2,0, 2,5, 3,0, 4,0, 5,0, 6,0, 8,0, 10,0.
Стандартный ряд II значительно расширяет диапазон применяемых на практике модулей ( m = 1,125, 1,375, 1,75 и т. д.).

При выборе модулей из стандартных рядов первый ряд следует предпочитать второму.

Высота головки и ножки зуба

Делительная окружность делит зуб по высоте на головку h_a и ножку h_f . Для создания радиального зазора с (см . рис. 1) необходимо

Для передачи без смещения h_a = m .

Длина активной линии зацепления

При вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S» пересечения линии зацепления с окружностью вершин шестерни.
Отрезок S’S» линии зацепления называют длиной активной линии зацепления и обозначают g_α . Длину g_α легко определить графически, для чего радиусами окружностей вершин обоих колес отсекают на линии зацепления NN отрезок S’S» и замеряют g_α .

Коэффициент торцового перекрытия

Коэффициентом торцового перекрытия ε_α называют отношение длины активной линии зацепления к основному шагу:

где z₁ и z₂ – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса.

Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи.

За период работ пары зубьев точка их зацепления проходит путь, равный по длине g_α (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу p_b . При g_α > p_b необходимое перекрытие зубьев обеспечивается.

По условию непрерывности зацепления должно быть ε_α > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия ε_α .

Зубчатые передачи стартера

Система допускаемых отклонений для зубчатых передач по «Стандарту межосевых расстояний» (DIN 3961) применяется в сило­вых приводах, где требуемый зазор между зубьями обеспечивается отрицательными допусками толщины зубьев. Эта система неприменима для зубчатых передач автомо­бильных стартеров, поскольку они работают со значительно большими зазорами между зубьями, которые обеспечиваются увеличе­нием межосевого расстояния.

Модули зубчатых передач стартеров

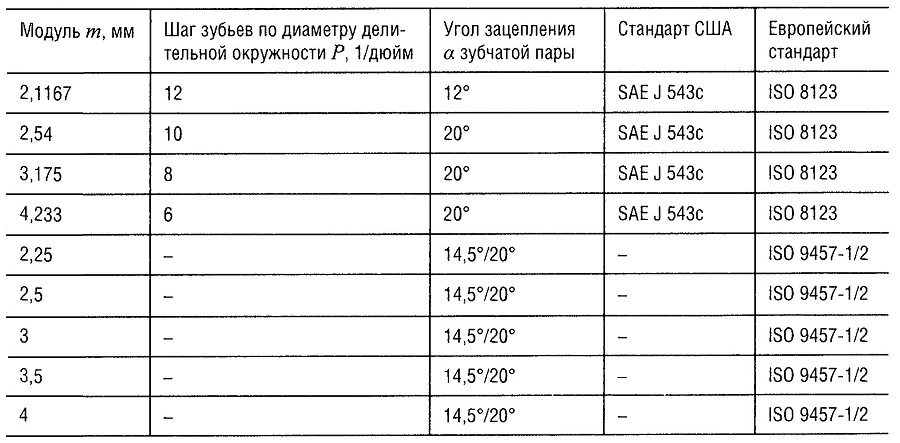
Большой крутящий момент, необходимый для пуска двигателя, требует применения зубчатой передачи с большим передаточным отношением (i = 10-20). Поэтому шестерня стартера имеет малое количество зубьев (z = 9-11), обычно с положительным смещением. Для шага зубьев принято следующее обозна­чение: количество зубьев, равное, например, 9/10, означает нарезку девяти зубьев на за­готовке, рассчитанной по диаметру на 10 зу­бьев, и соответствует смещению +0,5. При этом допускаются небольшие отклонения величины коэффициента х. (Это обозначе­ние нельзя смешивать с обозначением Р 8/10, приведенным ниже).

Зубчатая рейка

Зубчатая рейка является частью зубчатого колеса с бесконечным радиусом делительной окружности. Вследствие этого ее окружности представляют собой прямые параллельные линии. Эвольвентный профиль зубчатой рейки тоже имеет прямолинейное очертание. Это свойство эвольвенты является наиболее важным при изготовлении зубчатых колёс. Передачу с применением зубчатой планки (рейки) называют — реечная передача (кремальера), она используется для преобразования вращательного движения в поступательное и наоборот. Состоит передача из зубчатой рейки и прямозубого зубчатого колеса (шестеренки). Применяется такая передача в зубчатой железной дороге.

От автора. Я нашел в интернете полезную программку в Excel 2007. Это автоматизированная табличка для расчета всех параметров прямозубого зубчатого колеса.

Скачать Скачать с зеркала

Итак, приступим к графическому построению профиля зубчатого колеса.

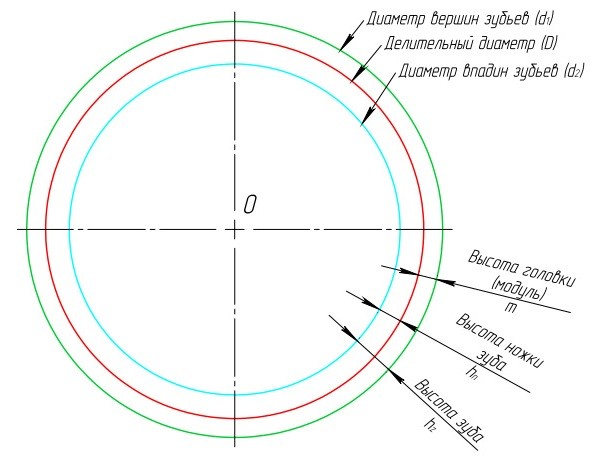
1. Изобразите делительный диаметр с диаметром D, и центром шестерни O. Окружность показана красным цветом.
2. Изобразите диаметр вершин зубьев (d₁) с центром в точке O с радиусом большим на высоту головки зуба(зелёного цвета).
3. Изобразите диаметр впадин зубьев (d2) с центром в точке O с радиусом меньшим на высоту ножки зуба (голубого цвета цвета).

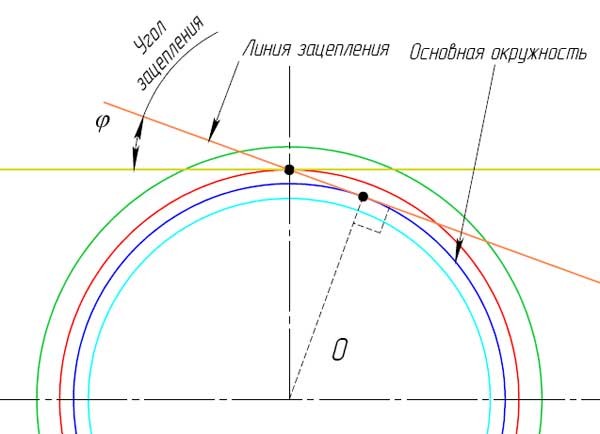
1. Проведите касательную к делительному диаметру (желтая).
2. В точке касания под углом ? проведите линию зацепления, оранжевого цвета.
3. Изобразите окружность касательную к линии зацепления, и центром в точке O. Эта окружность является основной и показана тёмно синего цвета.

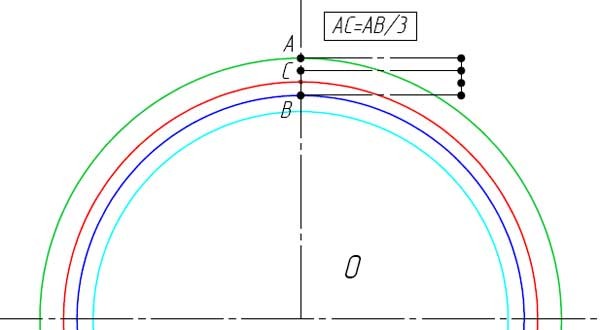
1. Отметьте точку A на диаметре вершин зубьев.
2. На прямой соединяющие точки A и O отметьте точку B находящуюся на основной окружности.
3. Разделите расстояние AB на 3 части и отметьте, точкой C, полученное значение от точки A в сторону точки B на отрезке AB.

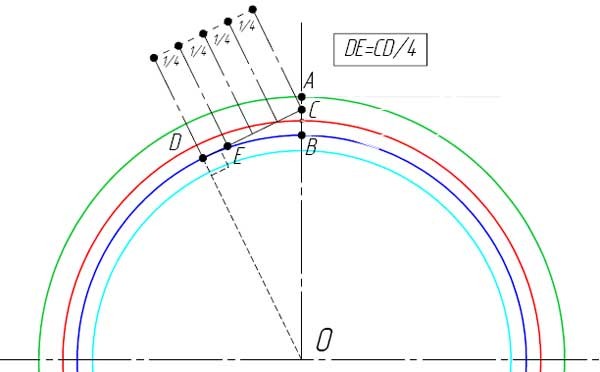
1. От точки C проведите касательную к основной окружности.
2. В точке касания отметьте точку D.
3. Разделите расстояние DC на четыре части и отметьте, точкой E, полученное значение от точки D в сторону точки C на отрезке DC.

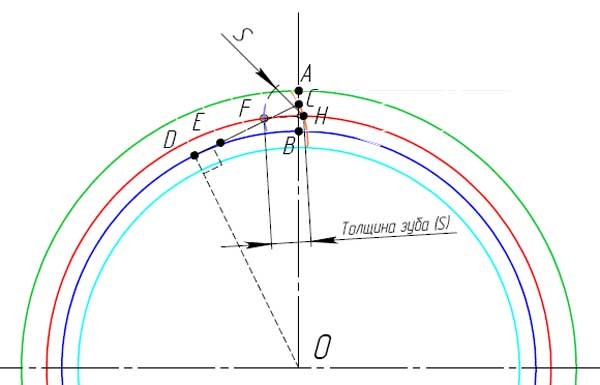
1. Изобразите дугу окружности с центром в точке E, что проходит через точку C. Это будет часть одной стороны зуба, показана оранжевым.
2. Изобразите дугу окружности с центром в точке H, радиусом, равным толщине зуба (s). Место пересечения с делительным диаметром отметьте точкой F. Эта точка находится на другой стороне зуба.

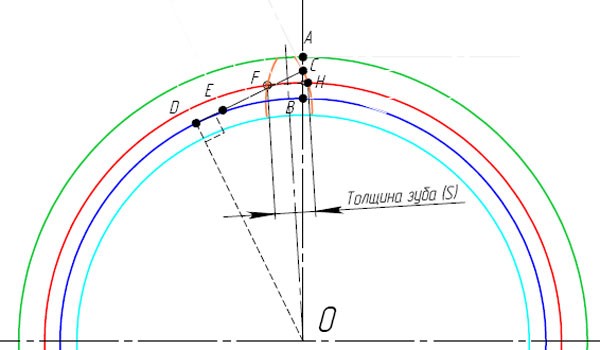
1. Изобразите ось симметрии проходящую через центр О и середину расстояния FH.
2. Линия профиля зуба отображенная зеркально относительно этой оси и будет второй стороной зуба.

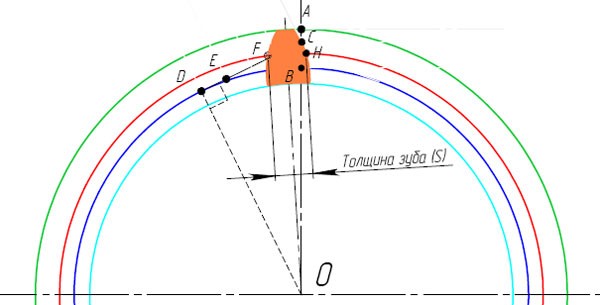
Вот и готов профиль зуба прямозубого зубчатого колеса. В этом примере использовались следующие параметры:

1. Модуль m=5 мм
2. Число зубьев z=20
3. Угол профиля исходного контура ?=20 0

1. Делительный диаметр D=100 мм
2. Диаметр вершин зубьевd₁=110 мм
3. Диаметр впадин зубьевd₂=87.5 мм
4. Толщина зубьев по делительной окружности S=7.853975 мм

На этом первая часть урока является завершенной. Во второй части (видео) мы рассмотрим как применить полученный профиль зуба для построения модели зубчатого колеса. Для полного ознакомления с данной темой («зубчатые колеса и зубчатые зацепления», а также «динамические сопряжения в SolidWorks») необходимо вместе с изучением этого урока изучать урок №24.

Еще скажу пару слов о специальной программе, производящей расчет зубчатых колес и генерацию модели зубчатого колеса для SolidWorks. Это программа Camnetics GearTrax.

P.S.(16.03.2010) Скачать Camnetics GearTrax

А теперь переходим с следующей части урока.

Скачать 2-ю часть урока №30 Скачать с зеркала

Винтовые, круговые, секторные версии

Модуль шестерни винтового типа представляет собой цилиндр с зубцами, которые размещены по винтовому направлению. Подобные элементы устанавливаются на непересекающиеся валы, расположенные перпендикулярно по отношению друг к другу. Угол совмещения составляет 90 градусов.

Секторное зубчатое колесо — часть любой шестерни, применяемая в передачах, где не нужно вращение основного элемента на полный оборот. Такая деталь дает возможность сэкономить ценное пространство в размерах полноценного аналога.

Шестерни по модулю и количеству зубьев с круговым расположением отличаются контактным соприкосновением в одной точке зацепления, расположенной параллельно основным осям. Второе название механизма — передача Новикова. Она обеспечивает хорошие ходовые характеристики, плавную и бесшумную работу, повышенную зацепляющую способность. При этом коэффициент полезного действия таких деталей немного ниже аналогов, а процесс изготовления существенно сложнее. Указанные детали имеют значительно ограниченную отрасль эксплуатации ввиду своих особенностей.

Содержание

• 1 Цилиндрические зубчатые колёса
  • 1.1 Продольная линия зуба
    • 1.1.1 Прямозубые колёса
    • 1.1.2 Косозубые колёса
    • 1.1.3 Шевронные колеса
  • 1.2 Зубчатые колёса с внутренним зацеплением
  • 1.3 Секторные колёса
  • 1.4 Колёса с круговыми зубьями
• 2 Конические зубчатые колёса
• 3 Реечная передача (кремальера)
• 4 Коронные колёса
• 5 Другие
• 6 Изготовление зубчатых колёс
  • 6.1 Метод обката
    • 6.1.1 Метод обката с применением гребёнки
    • 6.1.2 Метод обката с применением червячной фрезы
    • 6.1.3 Метод обката с применением долбяка
  • 6.2 Метод копирования (Метод деления)
  • 6.3 Горячее и холодное накатывание
  • 6.4 Изготовление конических колёс
  • 6.5 Моделирование
• 7 Ошибки при проектировании зубчатых колёс
  • 7.1 Подрезание зуба
  • 7.2 Заострение зуба
• 8 В природе
• 9 В геральдике
• 10 См. также
• 11 Ссылки
• 12 Примечания
• 13 Литература

Содержание

• 1 Цилиндрические зубчатые колёса
  • 1.1 Продольная линия зуба
    • 1.1.1 Прямозубые колёса
    • 1.1.2 Косозубые колёса
    • 1.1.3 Шевронные колеса
  • 1.2 Зубчатые колёса с внутренним зацеплением
  • 1.3 Секторные колёса
  • 1.4 Колёса с круговыми зубьями
• 2 Конические зубчатые колёса
• 3 Реечная передача (кремальера)
• 4 Коронные колёса
• 5 Другие
• 6 Изготовление зубчатых колёс
  • 6.1 Метод обката
    • 6.1.1 Метод обката с применением гребёнки
    • 6.1.2 Метод обката с применением червячной фрезы
    • 6.1.3 Метод обката с применением долбяка
  • 6.2 Метод копирования (Метод деления)
  • 6.3 Горячее и холодное накатывание
  • 6.4 Изготовление конических колёс
  • 6.5 Моделирование
• 7 Ошибки при проектировании зубчатых колёс
  • 7.1 Подрезание зуба
  • 7.2 Заострение зуба
• 8 В природе
• 9 В геральдике
• 10 См. также
• 11 Ссылки
• 12 Примечания
• 13 Литература

Чем отличается зубчатое колесо от шестерни

Еще один момент, на который следует обратить внимание. Конечно, в разговорной речи эти понятия идентичны, но с технической точки зрения шестерня отличается от зубчатого колеса. И различие в основном связано не с особенностями конструкции, а функцией, выполняемой в механизме.

Согласно перечню основных терминов, приведенных в ГОСТ 16530-83, шестерня — зубчатое колесо с меньшим числом зубьев для редукторов и большим числом для мультипликаторов. Если в механизм входят детали с одинаковым количеством зубьев, то шестерней считается ведущая деталь, а зубчатым колесом — ведомая. Отметим, что на практике применяется еще одна разновидность — вал-шестерня, которая представляет собой вал с нарезанными непосредственно на нем зубьями. Все перечисленные детали являются основными элементами механических зубчатых передач.

Обслуживание и расчёт

Техобслуживание заключается в осмотре механизма, проверке целостности зубьев и отсутствия сколов. Проверка правильности зацепления производится при помощи краски, наносимой на зубья. Изучается величина пятна контакта и его расположение по высоте зуба. Регулировка производится установкой прокладок в подшипниковых узлах.

Сначала надо определиться с кинематическими и силовыми характеристиками, необходимыми для работы механизма. Выбирается вид передачи, допустимые нагрузки и габариты, затем подбираются материалы и термообработка. Расчёт включает в себя выбор модуля зацепления, после этого подбираются величины смещений, число зубьев шестерни и колеса, межосевое расстояние, ширина венцов. Все значения можно выбирать по таблицам или использовать специальные компьютерные программы.

Главными условиями, необходимыми для длительной работы зубчатых передач, являются износостойкость контактных поверхностей зубьев и их прочность на изгиб.

Достижению хороших характеристик и уделяется основное внимание при проектировании и изготовлении зубчатых механизмов.