Гидростатическое давление

Физическая величина, равная отношению нормальной силы ($F$), действующей со стороны жидкости на некоторую площадь, на величину этой площади ($S$) называют давлением ($p$) жидкости:

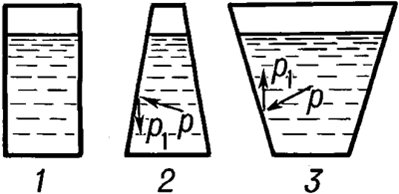
Если несжимаемая жидкость находится в равновесии давление по горизонтали всегда одно и то же. Свободная поверхность жидкости всегда горизонтальна, за исключением места около стенок сосуда. У несжимаемой жидкости плотность не зависит от давления. Если поперечное сечение цилиндрического столба жидкости равно $S$, высота столба $h$, плотность жидкости $rho $, тогда вес ($P$) этого столба равен:

[P=rho gSh left(2right).]

В соответствии с (1) давление на основание столба жидкости составит величину:

Формула (3) указывает, что давление столба несжимаемой жидкости на дно сосуда зависит от высоты и плотности жидкости. В общем случае плотность зависит от температуры жидкости. Давление, которое вычисляется при помощи формулы (3) называют гидростатическим давлением/

И так, гидростатическим давлением называют давление столба жидкости, находящейся в состоянии равновесия, над некоторым условно выбранным уровнем при действии силы тяжести. Гидростатическое давление определяется по формуле (3).

Давление внутри жидкости ($p$) на глубине $h$, будет складываться из давления атмосферы ($p_0$) и гидростатического давления:

Единицей измерения гидростатического давления в Международной системе единиц (СИ) является паскаль (Па):

От чего зависит параметр?

Для того чтобы рассчитать параметр давления в заданной точке, необходимо знать все о ее местоположении.

И учесть, что на усилие сжатия влияют следующие факторы:

плотность воды;
глубина погружения.

Может показаться странным, но размер и форма емкости на показатель ГДВ совершенно не влияют.

Сила тяжести

Гравитация — одна из четырех сил природы. Мощь гравитационной силы между двумя объектами зависит от массы этих объектов. Чем массивнее объекты, тем сильнее гравитационное притяжение.

Когда выливается вода из контейнера, гравитация Земли притягивает воду к земной поверхности. Можно наблюдать тот же самый эффект, если на разных высотах разместить два ведра воды и соединить их трубкой.

Достаточно задать ход жидкости в трубке из одного ведра в другой, после чего сработает сила гравитации, и процесс перелива продолжится самопроизвольно.

Гравитация, приложенные силы и атмосферное давление являются статическими факторами, которые в равной степени относятся к жидкостям, находящимся в покое или в движении.

Силы инерции и трения являются динамическими факторами, которые действуют только на жидкости в движении. Математическая сумма силы тяжести, приложенной силы и атмосферного давления, представляет собой статическое давление, полученное в любой зоне жидкости и в любой момент времени.

Гидравлический пресс

Гидравлический пресс состоит из двух сообщающихся сосудов цилиндрической формы. В сосудах двигаются поршни с площадями S₁ и S₂. Цилиндры заполнены техническим маслом.

Объем жидкости, вытесненный малым поршнем поступает в большой цилиндр.

Гидравлический пресс дает выигрыш в силе во столько раз, во сколько площадь большего поршня больше площади меньшего. Выигрыша в работе гидравлический пресс не дает.

На практике вследствие наличия трения:

Давление в толще жидкости

Допустим, мы нарастили сосуд снизу еще на некоторую величину, добавили дополнительное пространство для жидкости. Если мы поместим в емкость рыбку, давление на нее будет одинаковым в сосуде из предыдущего опыта и во втором, увеличенном? Изменится ли давление от того, что под рыбкой еще есть вода? Нет, потому что сверху находится определенный слой жидкости, на нее действует сила тяжести, значит, вода обладает весом. А то, что снизу, не имеет никакого значения. Следовательно, мы можем найти давление в самой толще жидкости, и h — это будет глубина. Она необязательно является расстоянием до дна, дно может быть и ниже.

Представим, что мы развернули рыбку на 90°, оставив ее на той же глубине. Изменится ли от этого давление на нее? Нет, потому что на глубине оно одинаково во всех направлениях. Если мы приблизим рыбку прямо к стенке сосуда, изменится ли давление на нее, если она будет оставаться на той же глубине? Нет. Во всех случаях давление на глубине h будет вычисляться по той же формуле. Значит, эта формула позволяет найти давление жидкости на дно и стенки сосуда на глубине h, т. е. в толще жидкости. Чем глубже, тем оно больше.

Ход урока

I. Организационный момент.

(На партах учащихся лежат рабочие карты урока, в которых представлены две самостоятельные работы и критерии выставления оценки; две ручки с разными стержнями, например синий и зеленый; таблицы плотностей веществ, учебники и тетради).

II. Актуализация знаний.

III. Объяснение нового материала

Провожу эксперимент: в пластмассовую бутылку с тремя отверстиями на разных уровнях по высоте наливаем подкрашенную воду.

Беседа с классом:

почему вода вытекает из сосуда?
сравните струи воды?
объясните, почему они разные?

Когда учащиеся объяснят, что столбы жидкости разные и давление на разной глубине разное, ставлю проблему: а нужно ли знать людям, чему равно давление жидкости на разных глубинах, на дно, на стенки сосуда?

Открываем тетради, записываем тему урока.

Ставим цель: вывести формулу для расчета давления жидкости на дно и стенки сосуда.

Давление жидкости (см. презентация)

Вокруг нас много жидкостей. Одни из них движутся, например, вода в реках или нефть в трубах, другие – покоятся. При этом все они имеют вес и поэтому давят на дно и стенки сосуда, в котором находятся. Подсчет давления движущейся жидкости – непростая задача, поэтому изучим лишь как рассчитывать давление, создаваемое весом покоящейся жидкости. Оно называется гидростатическим давлением и вычисляется по следующей формуле.


	p – давление слоя жидкости, Па
	ρ – плотность жидкости, кг/м3
	g – коэффициент, Н/кг
	h – высота слоя жидкости, м

Рассмотрим, как выведена эта формула. Сила F, с которой жидкость давит на дно сосуда, является весом жидкости. Его мы можем подсчитать по формуле F тяж = mg, так как жидкость и ее опора (дно сосуда) покоятся. Вспомним также формулу m = ρV для выражения массы тела через плотность его вещества и формулу V = Sh для подсчета объема тела, имеющего форму прямоугольного параллелепипеда. В результате имеем равенство:

Это равенство иллюстрирует не только способ вывода формулы для вычисления гидростатического давления. Оно также показывает, что формула p = ρgh является частным случаем определения давления – формулы p = F/S.

Заметим также, что при выводе формулы совсем необязательно предполагать, что слой высотой h и плотностью ρ образован именно жидкостью. В наших рассуждениях ничего не изменится, если вместо давления жидкости мы рассмотрим давление твердого тела прямоугольной формы или даже газа, заключенного в соответствующий сосуд. Создаваемое ими весовое давление будет именно таким, как предсказывает формула p = ρgh.

Формула p = ρgh показывает, что давление, создаваемое слоем жидкости, не зависит от ее массы, а зависит от плотности жидкости, высоты ее слоя и места наблюдения. При увеличении толщины слоя жидкости или ее плотности гидростатическое давление будет возрастать.

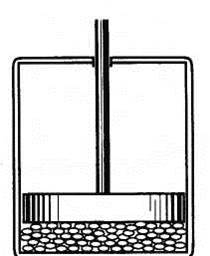
Полученный нами вывод можно проверить опытами. Проделаем их. Справа изображена стеклянная трубка с водой, дно которой затянуто тонкой резиновой пленкой. Увеличивая высоту слоя налитой жидкости, мы будем наблюдать увеличение растяжения пленки. Этот опыт подтверждает, что при увеличении высоты слоя жидкости создаваемое ею давление увеличивается.

На следующем рисунке изображены трубки с водой и «крепким» раствором соли. Видно, что уровни жидкостей находятся на одной и той же высоте, но давление на пленку в правой трубке больше. Это объясняется тем, что плотность раствора соли больше, чем плотность обычной воды.

На доске нарисован параллелепипед высотой h и площадью основания S. Предлагаю ребятам представить, что это аквариум, в котором налита вода. Попытаемся определять давление воды Р на дно аквариума. Работаем на магнитной доске с карточками, выкладывая поочередно формулы, получая цепочку: m=ρV, V=Sh, m=ρSh, P=gm, P=gρSh, ρ=P/S, p=ρgh.

Анализируем окончательную формулу: что же нужно знать, чтобы рассчитать давление жидкости.

Зависит ли давление от площади или формы сосуда?

Вьполняем фронтальный эксперимент: на каждой парте стоит стакан с водой. Высота налитой воды одинаковая.

Цель: определить давление воды на дно стакана.

Один ученик выполняет у доски. Остальные за партой. Сверяем ответ. Анализируем его: какую физическую величину мы измеряли? какую физическую величину брали в таблице? какое численное значение давления получили учащиеся, работающие за партой и у доски? большое это или маленькое давление?

IV. Закрепление изученного материала.

Приведи примеры движущихся жидкостей.

И движущиеся, и покоящиеся жидкости оказывают давление .
Гидростатическое давление — это .

Произведение в правой части формулы для вычисления гидростатического давления представляет собой .

По какой формуле мы сможем подсчитать вес покоящейся жидкости?
Объем слоя жидкости мы нашли при помощи произведения .
Выражение «p = . = ρgh» представляет собой .

О чем говорит равенство p=ρgh?
Как можно подтвердить справедливость формулы p=ρgh?

Увеличение растяжения пленки свидетельствует, что .
Описанный опыт иллюстрирует зависимость гидростатического давления от ..

Плотность раствора соли больше, чем плотность воды. Это приводит к тому, что .
Этот опыт иллюстрирует зависимость давления жидкости от ее плотности. Эта иллюстрация стала возможной благодаря тому, что .

а) Высота столба воды в стакане 8 см. Какое давление на дно стакана оказывает вода? Какое давление оказывала бы ртуть, если бы она была налита вместо воды?
б) Какое давление на дно сосуда оказывает слой керосина высотой 1,5 м?

в) Волк плывет под водой с дыхательной трубкой. Какие ограничения накладывает на ныряльщика дыхательная трубка? Ответ найдите в учебнике стр. 95.

Задача с недостающими данными

г) Какое давление на глубине 1,5 м? Решить устно.

Качественные задачи, предполагающие работу с дополнительными источниками информации

д) Какое преимущество дает ныряльщику акваланг? Какие ограничения он накладывает? Ответ в учебнике.

е) В следующем сюжете мы видим глубоководный аппарат. Почему у него такая внешняя форма?

ж) Чтобы человек мог работать на больших глубинах он должен находиться в специальном скафандре. Найдите о нем информацию в учебнике.

з) Анализируя рис. 103 учебника давайте познакомимся с тем, что говорит нам учебник о глубоководных аппаратах. Какие ограничения в их использовании имеются?

и) Вычислите, какое давление в самой глубокой Мариинской впадине глубиной.
к) В просмотренном сюжете мы видели с вами глубоководных рыб. Какую длину лески нужно приготовить для лова рыбы камбалы, если она может выдерживать давление 400 кПа.

V. Задаю домашнее задание:

параграф из учебника, упражнение на решение задач и сообщения:

«Человек изучает подводный мир».
«Подводные лодки, батисферы и батискафы».
«Животный мир океанских и морских глубин».
«Ныряльщики за жемчугом».

Что такое напор: характеризующие данные

Под размером гидростатического напора понимаются характерные свойства любой жидкости, состоящей в покое. Величину силы напора принято измерять метрами.

Данные определения напора выглядят следующим образом:

z – геометрический напор;
hp – пьезометрическая высота.

В основном гидростатический напор выражает размер энергии покоя любой жидкости. К примеру, от высоты водонапорной башни зависит сила напора, который поступает в водопроводную систему. Характеристика hp относится к размеру давления. Если появилось избыточное давление, значит, оно образовалось в водопроводе, следовательно, будет иметь место большой напор. Жидкость сможет подниматься на любую высоту.

Отсчет напора для разных точек жидкости производится от единой горизонтальной плоскости. Это необходимо для сравнения их положения. За горизонтальную поверхность может быть взята абсолютно любая поверхность. Если труба установлена горизонтально, в некоторых случаях расчет проводится относительно осевой линии трубы. В этом случае геометрическая высота становится нулем. Очень часто отметки высоты приравнивают к абсолютным геодезическим маякам, которые берут отсчет от усредненного уровня плоскости мирового океана. У нас в стране уровень отсчитывается от поверхности Балтийского моря.

Важнейшей особенностью гидростатического напора является его одинаковая величина относительно всех точек покоя воды, которые имеют гидравлическую связь. Расчет доказал, что сила напора равна на любой глубине, хотя давление может быть разным.

В открытом резервуаре величину напора точки водной поверхности найти очень просто. Нужно от горизонтальной поверхности замерить расстояние до открытого уровня воды, испытывающего атмосферное давление.

В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.

Жидкости подразделяют на два вида:

капельные
газообразные

Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами).

К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие

Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию.К газообразным жидкостям относятся все газы.

К основным физическим свойствам жидкости относятся:

Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.

Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.

Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.

Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях

Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.

В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.

Читайте также Как собрать люстру

Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.

Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.

Гидростатика

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением.

Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Гидростатическое давление обладает свойствами

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила – сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.8 ) и на ее свободную поверхность действует давление P . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

PdS – P dS – ρghdS = 0

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем:

P = P + ρgh = P + hγ

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Пьезометрический и гидростатический напоры

Рассмотрим закрытый сосуд с жидкостью, к которому в точках А и В на произвольной глубине присоединены пьезометры I и II (рис. 9).

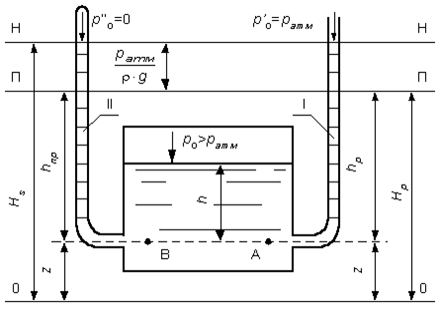
Давление на свободной поверхности в сосуде больше атмосферного. Трубка I сверху открыта и давление на свободной поверхности в ней равно атмосферному. Трубка II сверху запаяна, из нее удален воздух, т.е. давление в ней равно нулю.

Для определения вертикальных координат точек А и В проведем на произвольной высоте горизонтальную плоскость 0-0. Эта плоскость называется плоскостью сравнения. Вертикальное расстояние от плоскости сравнения до рассматриваемой точки называется геометрической высотой точки по отношению к плоскости сравнения и обозначается буквой. За плоскость сравнения может быть принят уровень земли, пола.

Так как давление в сосуде на свободной поверхности жидкости больше атмосферного, то в пьезометрических трубках I и II жидкость поднимется на большую высоту, чем уровень жидкости в сосуде. Обозначим высоту поднятия жидкости в открытом пьезометре через – пьезометрическая высота, а высоту поднятия жидкости в закрытом пьезометре через – приведенная высота.

Пьезометрическая высота – мера манометрического давления в точке А. Приведенная высота – мера абсолютного давления в точке В. Разность высот , равна высоте столба жидкости, соответствующей атмосферному давлению т.е. 10 м.в.ст.

Сумма геометрической высоты и пьезометрической для любой точки жидкости будет величиной постоянной и называется пьезометрическим напором:

Задачи

Скорость молекул в идеальном газе υ, масса одной молекулы газа – m, объем всего газа – V. Определить давление газа, если его плотность – $rho$.

Решение

Учитывая, что концентрация $n =$, запишем:

Открытый сосуд высотой 2 м на четверть заполнили водой. Определить полное давление на дно сосуда.

Запишем формулу полного давления:

$P = P_0 + rho gh$. Так как сосуд открытый, на него действует атмосферное давление.

Поэтому полное давление будет равно:

Гидростатическое давление