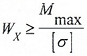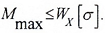Предел прочности при изгибе — Flexural strength

Предел прочности при изгибе — Flexural strength

Прочность на изгиб , также известный как модуль разрыва , или прочность на изгиб или прочность на разрыв поперечной это свойство материала, определяемое как стресс в материале непосредственно перед тем , дает при испытании на изгиб. Чаще всего используется испытание на поперечный изгиб, при котором образец, имеющий круглое или прямоугольное поперечное сечение, изгибается до разрушения или деформации с использованием метода испытания на трехточечный изгиб . Прочность на изгиб представляет собой максимальное напряжение, испытываемое материалом в момент его текучести. Он измеряется в единицах напряжения, здесь указан символ . σ < displaystyle sigma>

Прочность металлов

Физику прочности основал Галилей: обобщая свои опыты, он открыл (1638 г.), что при растяжении или сжатии нагрузка разрушения P для данного материала зависит только от площади поперечного сечения F. Так появилась новая физическая величина — напряжение σ=P/F — и физическая постоянная материала: напряжение разрушения [4].

Физика разрушения как фундаментальная наука о прочности металлов возникла в конце 40-х годов XX века [5]; это было продиктовано острой необходимостью разработки научно обоснованных мер для предотвращения участившихся катастрофических разрушений машин и сооружений. Раньше в области прочности и разрушения изделий учитывалась только классическая механика, основанная на постулатах однородного упруго-пластического твёрдого тела, без учёта внутренней структуры металла. Физика разрушения учитывает также атомно-кристаллическое строение решётки металлов, наличие дефектов металлической решётки и законы взаимодействия этих дефектов с элементами внутренней структуры металла: границами зёрен, второй фазой, неметаллическими включениями и др.

Большое влияние на прочность материала оказывает наличие ПАВ в окружающей среде, способных сильно адсорбироваться (влага, примеси); происходит уменьшение предела прочности.

К повышению прочности металла приводят целенаправленние изменения металлической структуры, в том числе — модифицирование сплава.

Учебный фильм о прочности металлов (СССР, год выпуска:

Предел прочности металла

Предел прочности меди. При комнатной температуре предел прочности отожжённой технической меди σ_В=23 кгс/мм 2 [8]. С ростом температуры испытания предел прочности меди уменьшается. Легирующие элементы и примеси различным образом влияют на предел прочности меди, как увеличивая, так и уменьшая его.

Предел прочности алюминия. Отожжённый алюминий технической чистоты при комнатной температуре имеет предел прочности σ_В=8 кгс/мм 2 [8]. С повышением чистоты прочность алюминия уменьшается, а пластичность увеличивается. Например, литой в землю алюминий чистотой 99,996% имеет предел прочности 5 кгс/мм 2 . Предел прочности алюминия уменьшается естественным образом при повышении температуры испытания. При понижении температуры от +27 до -269°C временное сопротивление алюминия повышается — в 4 раза у технического алюминия и в 7 раз у высокочистого алюминия. Легирование повышает прочность алюминия.

Предел прочности сталей

В качестве примера представлены значения предела прочности некоторых сталей. Эти значения взяты из государственных стандартов и являются рекомендуемыми (требуемыми). Реальные значения предела прочности сталей, равно как и чугунов, а также других металлических сплавов зависят от множества факторов и должны определяться при необходимости в каждом конкретном случае.

Для стальных отливок, изготовленных из нелегированных конструкционных сталей, предусмотренных стандартом (стальное литьё, ГОСТ 977-88), предел прочности стали при растяжении составляет примерно 40-60 кг/мм 2 или 392-569 МПа (нормализация или нормализация с отпуском), категория прочности К20-К30. Для тех же сталей после закалки и отпуска регламентируемые категории прочности КТ30-КТ40, значения временного сопротивления уже не менее 491-736 МПа.

Для конструкционных углеродистых качественных сталей (ГОСТ 1050-88, прокат размером до 80 мм, после нормализации):

• Предел прочности стали 10: сталь 10 имеет предел кратковременной прочности 330 МПа.
• Предел прочности стали 20: сталь 20 имеет предел кратковременной прочности 410 МПа.
• Предел прочности стали 45: сталь 45 имеет предел кратковременной прочности 600 МПа.

Категории прочности сталей

Категории прочности сталей (ГОСТ 977-88) условно обозначаются индексами «К» и «КТ», после индекса следует число, которое представляет собой значение требуемого предела текучести. Индекс «К» присваивается сталям в отожженном, нормализованном или отпущенном состоянии. Индекс «КТ» присваивается сталям после закалки и отпуска.

Предел прочности чугуна

Метод определения предела прочности чугуна регламентируется стандартом ГОСТ 27208-87 (Отливки из чугуна. Испытания на растяжение, определение временного сопротивления).

Предел прочности серого чугуна. Серый чугун (ГОСТ 1412-85) маркируется буквами СЧ, после букв следуют цифры, которые указывают минимальную величину предела прочности чугуна — временного сопротивления при растяжении (МПа*10 -1 ). ГОСТ 1412-85 распространяется на чугуны с пластинчатым графитом для отливок марок СЧ10-СЧ35; отсюда видно, минимальные значения предела прочности серого чугуна при растяжении в литом состоянии или после термической обработки варьируются от 10 до 35 кгс/мм 2 (или от 100 до 350 МПа). Превышение минимального значения предела прочности серого чугуна допускается не более, чем на 100 МПа, если иное не оговорено отдельно.

Предел прочности высокопрочного чугуна. Маркировка высокопрочного чугуна также включает в себя цифры, обозначающие временное сопротивление при растяжении чугуна (предел прочности), ГОСТ 7293-85. Предел прочности при растяжении высокопрочного чугуна составляет 35-100 кг/мм 2 (или от 350 до 1000 МПа).

Из вышеизложенного видно, что чугун с шаровидным графитом может успешно конкурировать со сталью.

Подготовлено: Корниенко А.Э. (ИЦМ)

Лит.:

1. Циммерман Р., Гюнтер К. Металлургия и материаловедение. Справ. изд. Пер. с нем. – М.: Металлургия, 1982. – 480 с.
2. Иванов В.Н. Словарь-справочник по литейному производству. – М.: Машиностроение, 1990. – 384 с.: ил. — ISBN 5-217-00241-1
3. Жуковец И.И. Механические испытания металлов: Учеб. для сред. ПТУ. — 2-е изд., перераб. и доп. – М.: Высш.шк., 1986. — 199 с.: ил. — (Профтехобразование). — ББК 34.2/ Ж 86/ УДЖ 620.1
4. Штремель М.А. Прочность сплавов. Часть II. Деформация: Учебник для вузов. — М.:*МИСИС*, 1997. — 527 с.
5. Мешков Ю.Я. Физика разрушения стали и актуальные вопросы конструкционной прочности // Структура реальных металлов: Сб. науч. тр. — Киев: Наук. думка, 1988. — С.235-254.
6. Френкель Я.И. Введение в теорию металлов. Издание четвёртое. — Л.: «Наука», Ленингр. отд., 1972. 424 с.
7. Получение и свойства чугуна с шаровидным графитом. Под редакцией Гиршовича Н.Г. — М.,Л.: Ленинградское отделение Машгиза, 1962, — 351 с.
8. Бобылев А.В. Механические и технологические свойства металлов. Справочник. — М.: Металлургия, 1980. 296 с.

Конкурс «Я и моя профессия: металловед, технолог литейного производства». Узнать, участвовать >>> —>

Виды пределов прочности

Предел прочности — один из главных механических параметров стали, равно как и любого другого конструкционного материала.

Эта величина используется при прочностных расчетах деталей и конструкций, судя по ней, решают, применим ли данный материал в конкретной сфере или нужно подбирать более прочный.

Различают следующие виды предела прочности при:

• сжатии — определяет способность материала сопротивляться давлению внешней силы;
• изгибе — влияет на гибкость деталей;
• кручении – показывает, насколько материал пригоден для нагруженных приводных валов, передающих крутящий момент;
• растяжении.

Виды испытаний прочности материалов

Научное название параметра, используемое в стандартах и других официальных документах — временное сопротивление разрыву.

Динамические испытания стальных образцов

Основной вид такого исследования – испытания на изгиб, производимые по ГОСТу 9454-78. При таком виде анализа стальных образцов закон подобия неактуален, поэтому используют образцы с размерами и формой надреза, строго соответствующими нормативам. Основной образец имеет квадратное сечение площадью 10х10 мм и следующие виды надрезов:

• U-образный (образцы Шарпи) – располагается в середине стержня. Такие образцы применяются для установления норм для стержней, на которые будет наноситься V-образный надрез.
• V-образный (образцы Менаже). Основной тип стальных стержней, применяемый для исследований материалов, которые будут использоваться в конструкциях ответственного назначения.
• С Т-образным концентратором. Размеры стержней имеют несколько вариантов. Такие образцы применяют при исследованиях сплавов, предназначенных для эксплуатации в конструкциях, в которых важным является сопротивление росту трещин.

В результате динамических испытаний на изгиб рассчитывают величину ударной вязкости – характеристики, которая зависит от сочетания прочностных и пластических свойств стали. Чем она выше, тем надежней материал работает при динамических нагрузках.

Все стали, изделия из которых предназначаются для эксплуатации при динамических нагрузках, подвергаются испытаниям на ударный изгиб. В зависимости от запланированных рабочих условий, ударную вязкость определяют при нормальных, пониженных или повышенных температурах.

Прочность древесины при сдвиге

Смещение в заготовке одной части древесины относительно другой называется сдвигом. Сдвиги образуются под действием внешних нагрузок разного характера. Выделяют сдвиги, возникающие от скалывания вдоль или поперек волокон и от распила (перерезания).

Прочность при скалывании меньше прочности продольного сжатия примерно в 5 раз. А если сравнивать прочность скалывания вдоль и поперек волокон в одном образце, то предел прочности при продольном скалывании в два раза выше, чем при поперечном. Прочность древесины при перерезании выше прочности при скалывании раза в четыре.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.

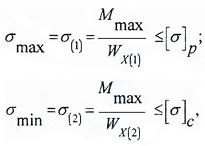
Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского

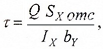
где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max:

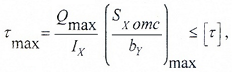
где [ τ] – допустимое значение касательных напряжений для материала балки.

Испытание цемента на прочность

От чего зависит прочность цемента? Данный материал представляет собой многокомпонентное вещество, и на прочность цементного камня после отвердения влияет:

• состав цемента;
• микроструктура минералов, из которых изготовлен материал;
• наличие добавок и их свойства.

К примеру, прочность белого цемента, который ценится за эстетичность и часто используется в декоративных целях (изготовление скульптур, декоративного кирпича, тротуарной плитки и т.д.) зависит от производителя. Датский завод Aalborg White производит материал прочностью 68-78 МПа, а российские заводы компании Holcim поставляют на рынок белый цемент прочностью 51-57 МПа.

Ход испытаний

Цемент набирает прочность в течение 28 суток после приготовления цементно-песчаного раствора. Для проведения испытаний материала изготавливают балочки стандартного формата 40х40х160 мм, при этом раствор готовят из расчета 1 часть цемента на 3 части однофракционного песка. Для определения прочности цемента разных классов испытания также проводятся через 2 или 7 суток твердения.

Класс прочности цемента	Прочность на сжатие, МПа, в возрасте
	2 сут, не менее	7 сут, не менее	28 сут
			не менее	не более
22,5Н	–	11	22,5	42,5
32,5Н	–	16	32,5	52,5
32,5Б*	10	–
42,5Н	10	–	42,5	62,5
42,5Б*	20	–
52,5Н	20	–	52,5	–
52,5Б*	30	–

Примечание: Н – нормированный, Б – быстротвердеющий.

Производители цемента обязаны указывать в паспорте продукции максимальную прочность цемента (результат испытаний после 28 суток твердения) и активность цемента, прошедшего процедуру пропаривания.

Пропаривание позволяет ускорить проверку показателей материала. Для этого:

• в камеру для пропаривания помещают формочки с цементно-песчаным раствором (габариты форм соответствуют габаритам стандартных балочек) и выдерживают в течение 5 часов;
• плавно, в течение 3 часов, поднимают температуру в камере до 80°С;
• выдерживают образцы при данной температуре на протяжении 8 часов;
• оставляют балочки на 2-3 часа остывать.

Остывшие сухие образцы подвергают испытаниям на гидравлическом прессе – проверяют на изгиб. Получившиеся в ходе проверки половинки балочек проверяют на сжатие. Средний результат сравнивается с актуальным ГОСТом и вносится в паспорт цемента.

Чтобы проверить, как цемент будет вести себя в бетоне, готовят образцы кубической формы (100х100х100 мм), при этом в раствор дополнительно вводятся химические добавки и щебень, и также испытывают при помощи гидропресса.

Понятие продольного изгиба

Продольным изгибом называется изгиб первоначально прямолинейного стержня вследствие потери устойчивости под действием центрально приложенных продольных сжимающих сил. Продольный изгиб возникает при достижении сжимающими силами и напряжениями критического значения.

Расчеты на прочность и жесткость, выполняемые для большинства видов деформаций основываются на предположении, что между внешними нагрузками и вызываемыми ими внутренними силами существует устойчивая форма равновесия, при которой малым возмущающим воздействиям соответствуют малые отклонения конструкции от первоначальной формы.
Нагрузки, при превышении которых происходит потеря устойчивости (критическое состояние), называют критическими нагрузками.

Примером явления продольного изгиба может послужить длинная школьная линейка, к одному из концов которой приложена сжимающая сила. Сначала материал линейки сопротивляется нагрузке, и линейка работает, как обычный сжимаемый брус. Затем, по достижении определенной нагрузки, линейка начинает прогрессирующе изгибаться без существенного увеличения сжимающей силы и теряет устойчивость (т. е. гнется без заметных усилий вплоть до поломки).

Явление продольного изгиба можно объяснить тем, что к реальному стержню практически невозможно применить основные гипотезы и допущения сопромата — об однородности, изотропности и непрерывности материала. Поэтому при продольном сжатии стержня, даже если сжимающая сила приложена идеально вдоль его оси (что тоже на практике нереально), отдельные волокна этого стержня неодинаково сопротивляются сжатию (из-за неоднородности и анизотропии материала, из которого он изготовлен). В результате, при достижении сжимающей силой критической величины, стержень начинает изгибаться в сторону наименьшего сопротивления волокон.
На практике этому способствует, также, приложение нагрузки не строго вдоль центральной оси сечения. По мере увеличения изгиба и потери стержнем устойчивости возрастают изгибающие нагрузки, поскольку, чем сильнее изгибается стержень, тем дальше от его оси отклоняется линия действия сжимающей силы, образуя возрастающий момент изгиба. По этой причине стержень изгибается все сильнее даже при небольшом возрастании сжимающей силы (прогрессивно растет плечо изгибающего момента этой силы).
В конечном итоге стержень теряет устойчивость, что чаще всего сопровождается его поломкой или неупругой деформацией (безвозратной потерей прямолинейности или начальной формы).

Если предположить, что материал стержня идеально соответствует принимаемым в сопромате допущениям и гипотезам, а сжимающая сила приложена строго к центру тяжести сечения вдоль оси стержня, то такой стержень будет работать на простое сжатие, и разрушится не из-за потери устойчивости, а из-за превышения предельных прочностных характеристик для сжатия. Если же стержень имеет сечение в виде сложной фигуры, то решающую роль при потере устойчивости играет отклонение продольной нагрузки от главной центральной оси этой фигуры.

Опасность потери устойчивости особенно велика для тонкостенных конструкций, стержней, пластинок и оболочек.

Рассмотрим тонкий стальной стержень, длина которого значительно больше поперечных размеров, сжимаемый силой F , немного большей критической силы F_кр (см. рисунок 1) .

Применяя метод сечений, убеждаемся, что в результате искривления оси в поперечных сечениях стержня возникают два внутренних силовых фактора – продольная сила N = F и изгибающий момент М_и .

Таким образом, искривленный стержень испытывает сочетание деформаций центрального сжатия и изгиба.

При сжимающих силах, даже немного превышающих критическую силу, напряжения изгиба могут непосредственно угрожать прочности конструкции. Поэтому критическое состояние конструкции считается недопустимым.

Для обеспечения устойчивости необходимо, чтобы действующая на стержень сжимающая сила F была меньше критической F_кр . Обозначим допускаемую сжимающую силу [F] , тогда:

где: [s_y] – допускаемый коэффициент запаса устойчивости.

Очевидно, что устойчивость стержня обеспечена, если [s_y] > 1.

Значение коэффициента запаса устойчивости зависит от назначения стержня и его материала. Обычно для сталей [s_y] = 1,8….3; для чугунов [s_y] = 5….5,5; для дерева [s_y] = 2,8….3,2.

Формулы Эйлера и Ясинского для расчетов стержней на устойчивость

Первые исследования устойчивости сжатых стержней были проведены академиком Петербургской Академии наук Леонардом Эйлером (1707-1783 г.г.). В дальнейшем большая работа в области теоретического и экспериментального следования вопросов устойчивости была проведена русским ученым, профессором Петербургского института инженеров путей сообщения Ф. С. Ясинским (1856-1899 г.г.), опубликовавшим в 1893 году научную работу «Опыт развития продольного изгиба».

Леонард Эйлер (Leonhard Euler, 1707 — 1783) — выдающийся ученый, которого в разных источниках называют швейцарским, немецким и российским. Математик, физик, астроном и механик, внёсший фундаментальный вклад в развитие этих и ряда других прикладных наук.
Эйлер — автор более чем 850 научных работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.
Академик Петербургской, Берлинской, Туринской, Лиссабонской и Базельской академий наук, иностранный член Парижской академии наук.

Л. Эйлер почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1726 по 1741, а также с 1766 года и до конца жизни был академиком Петербургской академии наук. С 1741 по 1766 год работал в Берлине (оставаясь одновременно почётным членом Петербургской академии).
Превосходно знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском.
Некоторые из потомков Л. Эйлера до сих пор живут в России.

Л. Эйлером была предложена формула для определения величины критической силы F_кр , которая приводится здесь без вывода:

где: Е – модуль упругости первого рода; I_min — наименьший из осевых моментов инерции сечения, поскольку искривление происходит в плоскости наименьшей жесткости; l_п – приведенная длина стержня, которая может быть определена по формуле:

где: l – длина стержня; μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня.

Наиболее часто встречающиеся способы закрепления концов стержня и соответствующие им значения коэффициента приведения длины представлены на рисунке 2 .

Вывод формулы Эйлера основан на известном законе Гука, который справедлив лишь до предела пропорциональности. Поэтому формулой Эйлера можно пользоваться не всегда.
Для определения пределов применимости формулы Эйлера определим критическое напряжение σ_кр , т. е. напряжение, которое возникает в поперечном сечении площадью А стержня при достижении критической силы:

Определим наименьший радиус инерции i_min поперечного сечения стержня:

i_min = √(I_min / A) (здесь √ — знак квадратного корня) .

Перепишем формулу для σ_кр так:

Введем понятие гибкости стержня: λ = μl / i_min . Это безразмерная величина, характеризующая размеры стержня и способ закрепления его концов. Окончательно получим:

σ_кр = π 2 Е / λ 2 .

Формулу Эйлера можно применять только при выполнении условия:

где: σ_пц – предел пропорциональности материала стержня. Следовательно, должно быть

λ ≥ √( π 2 Е / σ_пц) = λ_пред (здесь √ — знак квадратного корня) .

Величину, стоящую в правой части неравенства, называют предельной гибкостью. Предельная гибкость зависит только от физико-механических свойств материала стержня.
Условие применимости формулы Эйлера можно записать так: λ ≥ λ_пред , т. е. формула Эйлера применима лишь в тех случаях, когда гибкость стержня больше или равна предельной гибкости. Так, для стержней из низкоуглеродистой стали формула Эйлера применима, если их гибкость λ ≥ 100.

В тех случаях, когда гибкость стержней меньше предельной, формула Эйлера становится неприменимой и при расчетах пользуются эмпирической формулой Ясинского:

где: а и b – коэффициенты, зависящие от материала и определяемые по таблицам справочников.

Если стержень имеет гибкость λ ≤ 40, то его можно рассчитывать на простое сжатие по формуле σ_с = F / А .

Расчеты прямолинейных стержней на устойчивость

Существует три вида расчетов на устойчивость прямолинейных стержней – проектный, проверочный и силовой.

Проектный расчет заключается в определении минимального осевого момента инерции поперечного сечения стержня по формуле:

где: F — действующая нагрузка; [s_y] – допускаемый коэффициент запаса устойчивости; μ – коэффициент приведения длины стержня; l – длина стержня; Е – модуль продольной упругости.

Далее находят гибкость стержня по формуле: λ = μl / i_min ,

где: i_min = √(I_min / A) , ( А – площадь сечения стержня) .

Полученную гибкость сравнивают с предельной для данного материала.

Проверочный расчет заключается в определении действительного коэффициента запаса устойчивости s_y и сравнении его с допускаемым:

Силовой расчет заключается в определении допускаемой нагрузки [F] по формуле:

Расчет сжатых стержней на устойчивость можно свести к расчету на простое сжатие. При расчете применяют следующую формулу:

где: [σ_с] – допускаемое напряжение на сжатие; φ – коэффициент продольного изгиба (справочная величина, определяемая по таблицам).

Расчеты показывают, что при продольном изгибе наиболее выгодными являются кольцевые и коробочные тонкостенные сечения, имеющие относительно большой момент инерции.

При покупке листов ГВЛ советуем руководствоваться простыми, но эффективными правилами. Приобретайте товар только от известных производителей, хорошо зарекомендовавших себя на российском рынке.

Даже если их продукт будет несколько дороже, советуем не мелочиться. Гипсоволокно низкого качества доставит вам много хлопот и не позволит сделать ремонт на высоком уровне. Придется, скорее всего, платить дважды.

Обращайте внимание на маркировку каждого листа, поскольку внешне они ничем не отличаются от обычных плит.