Уроки по SolidWorks
Уроки по SolidWorks
 |
УГОЛОК ПОСЕТИТЕЛЯ  |
Журнал САПР  |
ВСЕ ВИДЕОУРОКИ  |

| Урок №30. Построение эвольвенты зубчатого колеса (упрощенный способ) |
detector
| Автор: Петр Марценюк | ||
| 29.11.2009 14:05 | ||
|
Часто задаваемые вопросы: *Что такое эвольвента (эволюта)? Итак, начнем с теории. Эвольвентное зацепление позволяет передавать движение с постоянным передаточным отношением. Эвольвентное зацепление — зубчатое зацепление, в котором профили зубьев очерчены по эвольвенте окружности.
Параметры зубчатых колёсОсновной теореме зацепления удовлетворяют различные кривые, в том числе эвольвента и окружность, по которым чаще всего изготавливают профили зубьев зубчатого колеса. В случае, если профиль зуба выполнен по эвольвенте, передача называется эвольвентной. Для передачи больших усилий с помощью зубчатых механизмов используют зацепление Новикова, в котором профиль зуба выполнен по окружности. Окружности, которые катятся в зацеплении без скольжения друг по другу, называются начальными (D). Окружности, огибающие головки зубьев зубчатых колёс, называются окружностями головок (d1). Окружности, огибающие ножки зубьев зубчатых колёс, называются окружностями ножек (d2). Окружности, по которым катятся прямые, образующие эвольвенты зубьев первого и второго колёс, называются основными окружностями. Окружность, которая делит зуб на головку и ножку, называется делительной окружностью (D). Для нулевых (некорригированных) колёс начальная и делительная окружности совпадают. Расстояние между одноимёнными точками двух соседних профилей зубьев зубчатого колеса называется шагом по соответствующей окружности. Шаг можно определить по любой из пяти окружностей. Чаще всего используют делительный шаг p =2
Модуль зубчатого колеса, геометрический параметр зубчатых колёс. Для прямозубых цилиндрических зубчатых колёс модуль m равен отношению диаметра делительной окружности (D) к числу зубьев z или отношению шага p к числу «пи»
Модуль зубчатого колеса стандартизованы, что является основой для стандартизации других параметров зубчатых колёс. Основные формулы для расчета эвольвентного зацепления:Исходными данными для расчета как эвольвенты, так и зубчатого колеса являются следующие параметры: m — Модуль — часть диаметра делительной окружности приходящаяся на один зуб. Модуль — стандартная величина и определяется по справочникам. z — количество зубьев колеса. ? («альфа») — угол профиля исходного контура. Угол является величиной стандартной и равной 20°. Делительный диаметр рассчитывается по формуле: Диаметр вершин зубьев рассчитывается по формуле: Детали машинЭвольвентное зацепление зубчатых колес характеризуется различными геометрическими параметрами, оказывающими существенное влияние на свойства и работу передачи. К таким параметрам относятся диаметры начальной, основной и делительной окружностей, окружной шаг зубьев, модуль зацепления, высота головок и ножек зубьев, длина активной линии зацепления, угол наклона линии зуба косозубого колеса, коэффициент перекрытия и некоторые другие. В обозначении геометрических параметров зацепления используют индексы, относящиеся к характерным окружностям зубчатых колес:
Параметрам, относящимся к делительной окружности, индекс не присваивается. При обозначении параметров пары зубчатых колес индекс «1» присваивается шестерне, «2» — колесу. Начальные окружностиНачальными называют окружности, которые в процессе зацепления перекатываются одна по другой без скольжения (рис. 1), при этом отношение их радиусов (расстояний от центров О1 и О2 до полюса П ) при неизменном межосевом расстоянии О1О2 тоже остается неизменным. Межосевое расстояние определяется по формуле:
Делительная окружностьОкружность, на которой шаг p и угол зацепления α соответственно равны шагу p и углу α профиля инструментальной рейки, называют делительной окружностью (рис. 1). Эта окружность принадлежит отдельно взятому колесу, ее диаметр d при изменении межосевого расстояния остается неизменным. Делительные окружности совпадают с начальными, если межосевое расстояние пары зубчатых колес равно сумме радиусов делительных окружностей. У большинства зубчатых передач диаметры делительных и начальных окружностей совпадают, т. е.: Исключение составляют передачи с угловой модификацией. Окружной шаг зубьевРасстояние между одноименными сторонами двух соседних зубьев, взятое по дуге делительной окружности, называют окружным шагом зубьев по делительной окружности и обозначают буквой p (рис. 1). Основной шагЭтот параметр, обозначаемый pb , относится к основной окружности. На основании второго и четвертого свойств эвольвенты расстояние по нормали между одноименными сторонами двух соседних зубьев равно шагу pb . Окружная толщина зуба и окружная ширина впадиныОкружная толщина зуба st и окружная ширина впадины et по дуге делительной окружности колеса передачи без смещения теоретически равны. Однако при изготовлении зубчатых колес на теоретический размер st назначают такое расположение поля допуска, при котором зуб получается тоньше, чем и гарантируется боковой зазор j (рис. 1), необходимый для нормального зацепления. По делительной окружности всегда st + et = p . Окружной модуль зубьевИз определения окружного шага следует, что длина делительной окружности зубчатого колеса πd = pz , где z – число зубьев. Следовательно, Шаг зубьев p , так же как длина окружности, включает в себя трансцендентное число π , а поэтом шаг — также число трансцендентное. Для удобства расчетов и измерения зубчатых колес в качестве основного расчетного параметра принято рациональное число p/π , которое называют модулем зубьев , обозначают m и измеряют в миллиметрах: d = mz или m = d/z . Модуль зубьев m – часть диаметра делительной окружности, приходящаяся на один зуб. Модуль является основной характеристикой размера зубьев. Для пары зацепляющихся колес модуль должен быть одинаковым. Для обеспечения взаимозаменяемости зубчатых колес и унификации дорогостоящего зубонарезного оборудования и инструмента значения m регламентируются стандартом в диапазоне от 0,05 до 100 мм. При выборе модулей из стандартных рядов первый ряд следует предпочитать второму. Высота головки и ножки зубаДелительная окружность делит зуб по высоте на головку ha и ножку hf . Для создания радиального зазора с (см . рис. 1) необходимо Для передачи без смещения ha = m . Длина активной линии зацепленияПри вращении зубчатых колес точка зацепления S (см. рис. 1) пары зубьев перемещается по линии зацепления NN . Зацепление профилей начинается в точке S’ пересечения линии зацепления с окружностью вершин колеса и заканчивается в точке S» пересечения линии зацепления с окружностью вершин шестерни.
Коэффициент торцового перекрытияКоэффициентом торцового перекрытия εα называют отношение длины активной линии зацепления к основному шагу: где z1 и z2 – числа зубьев шестерни и колеса; β – угол наклона линии зуба косозубого колеса. Непрерывность работы зубчатой передачи возможна при условии, когда последующая пара зубьев входит в зацепление до выхода предыдущей, т. е. когда обеспечивается перекрытие работы одной пары зубьев другой. Чем больше пар зубьев одновременно находится в зацеплении, тем выше плавность работы передачи. За период работ пары зубьев точка их зацепления проходит путь, равный по длине gα (см. рис. 1), а расстояние между профилями соседних зубьев по линии зацепления равно основному шагу pb . При gα > pb необходимое перекрытие зубьев обеспечивается. По условию непрерывности зацепления должно быть εα > 1. С увеличением количества зубьев z увеличивается и коэффициент торцового перекрытия εα . Формула расчета параметров прямозубой передачиЧтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.
Расчет модуля зубчатого колеса Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину: проведя преобразование, получим: Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m. размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится: выполнив преобразование, находим: Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным где h’- высота головки. Высоту головки приравнивают к m: Проведя математические преобразования с подстановкой, получим: Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца: где h“- высота ножки зубца. Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:
Устройство зубчатого колеса Выполнив подстановку в правой части равенства, имеем: что соответствует формуле: и если выполнить подстановку, то получим: Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25. Следующий важный размер, толщину зубца s принимают приблизительно равной:
Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины
Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:
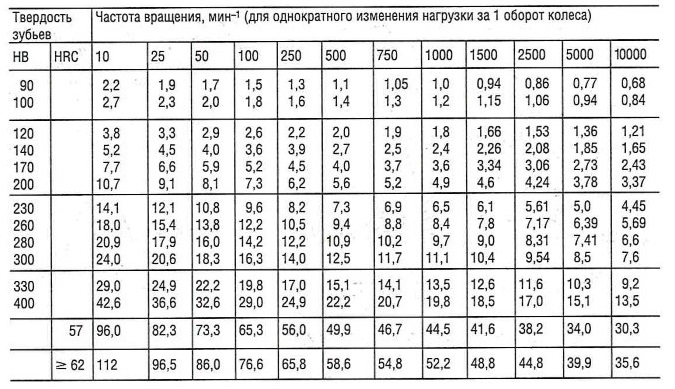
Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров. Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес. Расчет наибольшего допустимого давления зубчатых передачНиже приведены расчетные формулы, которые могут применяться вместо стандартного расчета DIN 3990 «Расчет несущей способности зубчатых передач». Эти зависимости применимы для расчета нагрузки трансмиссионных зубчатых пар, работающих в стандартном режиме. Величины и единицы измерения для расчета наибольшего допустимого давления
Необходимое сопротивление усталостному выкрашиванию и изнашиванию металла для шестерни (колесо 1) вследствие высокого контактного давления достигается, если величина оценки сопротивления выкрашиванию Sw равна или больше 1. В случае зубчатого зацепления с z1 2 для срока службы Lh = 5000 ч
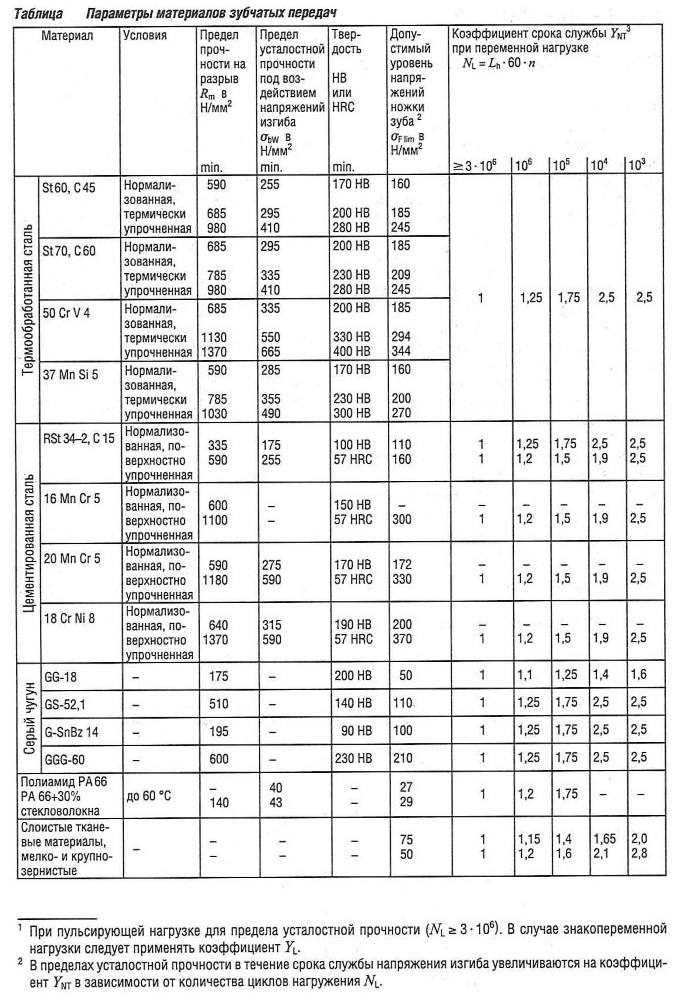
Прочностные характеристики материалов для изготовления зубчатых передач приведены в табл. «Параметры материалов зубчатых передач«.
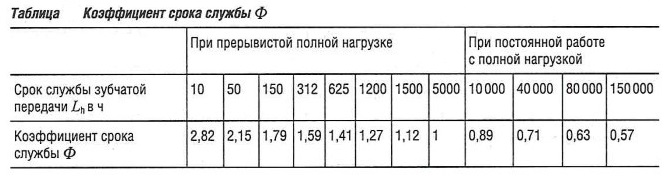
Коэффициент срока службы фКоэффициент срока службы используется для корректирования приведенных в верхней таблице значений коэффициента допустимого контактного давления kperm (рассчитанного на срок службы Lh = 5000 ч) для различной расчетной продолжительности работы зубчатой передачи.
Рекомендации по выбору расчетного срока службы зубчатых передач: при постоянной работе с полной нагрузкой — от 40 000 до 150 000 ч; при прерывистой полной нагрузке — от 50 до 5000 ч. Необходимая величина сопротивления разрушению зуба обеспечивается при SF ⩾ 1 для шестерни (колесо 1). Если шестерня изготовлена из более прочного материала, чем зубчатое колесо 2, следует также произвести проверочный расчет зубчатого колеса на изгибающие нагрузки. Содержание
Модуль конической шестерниЭтот тип зубчатых колес имеет различные разновидности, которые между собой отличаются конфигурацией линий зубцов: прямые, криволинейные, тангенциальные, круговые элементы. Подобные детали используются в агрегатах для трансформации движения механизма посредством передачи эффекта движения с одного на другой вал. К примеру, в дифференциалах автомобилей при трансформации крутящего момента с силового агрегата на колеса.
Конические шестерни по модулю и количеству зубьев подразделяются следующим образом:
Что такое модуль зуба шестерниМодуль зуба шестерни — один из основных параметров, на который следует обращать внимание при выборе. Это универсальная линейная характеристика, позволяющая связать воедино все основные параметры шестерни — количество зубьев и их высоту, шаг, диаметр делительной окружности шестерни. Именно от этого показателя прочность шестерни, чем большим будет модуль, тем меньше зубья подвержены износу, благодаря чему существенно увеличивается рабочий ресурс детали. Модуль зацепления шестерни может быть рассчитан по нескольким формулам. Чаще всего используют отношение шага зубьев к числу Пи. Но это значение можно выразить и через высоту зуба, при этом модуль будет в 2,25 раз меньше высоты. Нередко для расчета определяют значение делительного диаметра и делят его на количество зубьев, увеличенное на 2. Изготовление зубчатых передач, отличающихся по модулюНТЦ Редуктор изготавливает зубчатые передачи, зубчатые шестерни и зубчатые колеса, отличающиеся по размеру модуля зубьев, а именно:
Модуль…от М=0.2 мм до М=1.0 мм
Модуль…от М=1.0 мм до М=10 мм Модуль…от М=10 мм до М=25 мм Модуль…от М=25 мм до М=60 мм Все эти четыре разновидности зубчатых передач, отличающиеся по размеру модуля зуба, изготавливаются на разных зубообрабатывающих станках. Наиболее распространены в промышленности зубчатые передачи, зубчатые шестерни и зубчатые колеса со средним значением модуля. Соответственно, для нарезания таких зубьев применяются широко распространенные и производимые в России зубообрабатывающие станки-зуборезные, зубошевинговальные, зубошлифовальные. Для обработки мелкомодульных зубчатых передач, а также передач крупного модуля требуются специальные, менее распространенные в России станки. НТЦ «Редуктор» располагает станками для изготовления мелкомодульных зубчатых передач. Для обработки зубчатых передач, зубчатых шестерен и зубчатых колес особо крупного модуля, до М=35 мм, НТЦ Редуктор применяет имеющиеся уникальные станки, типа 5А342П, а для модулей свыше М=35 мм, применяются специальные станки и специальные способы обработки зубьев зубчатых колес. ИЗГОТОВЛЕНИЕ ЗУБЧАТЫХ ПЕРЕДАЧ, ОТЛИЧАЮЩИХСЯ ПО ТОЧНОСТИНТЦ «Редуктор» принимает заказы на изготовление цилиндрических зубчатых передач (краткая форма термина — зубчатые передачи) в широком диапазоне точности их изготовления, от крайне низкой, до особо высокой степени точности. Такая конструкторская и технологическая идеология своими корнями уходит во времена Советского Союза, когда стремились к максимальной простоте и дешевизне изготовления, в том числе и при изготовлении зубчатых передач. Да, зубчатые передачи, шестерни и колеса, изготавливаемые из-под фрезы дешевые, что привлекательно для потребителей зубчатых передач, которые нацелены на максимальную дешевизну и не нацелены на высокое качество и долговечность эксплуатации. И такие тенденции в России по-прежнему очень сильны и устойчивы. Хотя и они сегодня стремительно меняются. Меняются, потому что промышленную Россию «наводнили» зубчатые передачи, шестерни и колеса, изготовленные зарубежными фирмами. И все эти зарубежные изделия характеризуются заметно лучшими эксплуатационными свойствами: повышенными передаваемыми нагрузками, заметно пониженным шумом и значительно повышенной эксплуатационной долговечностью. Это видят потребители и поэтому все чаще отказываются от дешевизны, вспоминая А. С. Пушкина и его «не гонялся бы ты, поп, за дешевизной». И предпочитают более совершенные, пусть и более дорогие, зубчатые передачи, шестерни и колеса. Различают по точности зубчатые передачи, шестерни и колеса:—крайне низкой точности, 10-я…12-я степени точности В зависимости от точности зубчатые передачи, зубчатые шестерни и зубчатые колеса изготавливаются по различным технологическим процессам, с применением разного оборудования. Зубчатые передачи, шестерни и колеса 7-й степени точности изготавливают двояко… Зубчатые передачи, шестерни и колеса 5-й…6-й степеней точности предварительно нарезают червячной фрезой, оставляя припуск на окончательную шлифовку зубьев, которую выполняют после их закалки до высокой твердости, от 54 до 61 HRCэ. Работают такие зубчатые передачи бесшумно. Работоспособность и точность таких передач и колес повышается в 3…5 и более раз. Применяют такие зубчатые передачи при повышенных скоростях вращения. Особо точные зубчатые передачи, шестерни и колеса 3-й…4-й степеней точности применяются при очень высоких угловых скоростях вращения, от 3000 до 100000 об/мин.
ИЗГОТОВЛЕНИЕ ЗУБЧАТЫХ ПЕРЕДАЧ, ОТЛИЧАЮЩИХСЯ ПО ТВЕРДОСТИ ПОВЕРХНОСТЕЙ =============================================================================== Зубчатая передача — это механизм, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей и моментов. Зубчатая пара состоит из шестерни и колеса. В большинстве случаев шестерня является ведущим элементом зубчатой пары, а колесо — ведомым, хотя встречается и обратное соотношение. Обычно шестерня имеет меньший диаметр. Как правило, при рассмотрении одинаковых параметров шестерни и колеса, шестерне присваивают индекс 1, колесу -2. Например, Z1 — количество зубьев шестерни. Z2 — количество зубьев колеса. |
 Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.
Урок посвящен построению зубчатого колеса с эвольвентным профилем зуба. Урок состоит из двух частей. В первой части выложена теория, формулы для расчета и один из способов графического построения эвольвентного профиля зуба.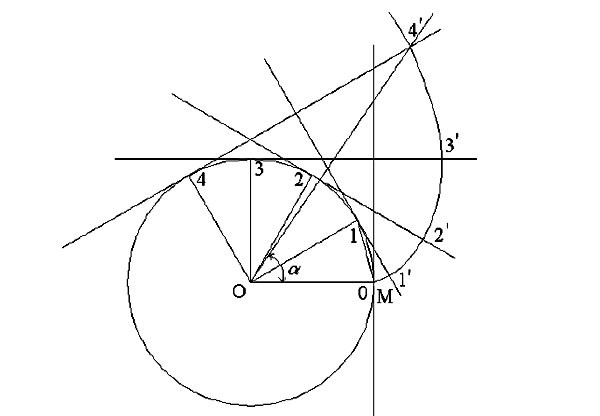
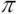 r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный
r/z, где z – число зубьев зубчатого колеса. Чтобы уйти от иррациональности в расчётах параметров зубчатых колёс, в рассмотрение вводят модуль, измеряемый в миллиметрах, равный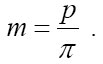







 Производственное оборудование для изготовления шестерен
Производственное оборудование для изготовления шестерен