Значение слова; объём

Значение слова «объём»

ОБЪЁМ, -а, м.

1. Величина чего-л. в длину, высоту и ширину, измеряемая в кубических единицах. Объем геометрического тела. Объем куба. Объем здания.

2. Содержание чего-л. с точки зрения величины, размеров, количества и т. п. Объем работ. Объем розничной торговли. Объем знаний. Объем информации. □ Литературное наследство Гаршина очень невелико по объему. Короленко, В. М. Гаршин.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

• Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами. С понятием объёма тесно связано понятие вместимость, то есть объём внутреннего пространства сосуда, упаковочного ящика и т. п.

Единица измерения объёма в СИ — кубический метр; от неё образуются производные единицы, такие как кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель.

В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».

Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.

ОБЪЁМ, а, м. 1. Величина в длину, ширину и высоту какого-н. тела с замкнутыми поверхностями, измеряемая в кубических единицах. О. шара. О. комнаты равен 140 куб. метрам. О. воды увеличивается при нагревании. 2. Величина, размеры. Книга небольшого объема. О. капитальных вложений в промышленность. || Содержание чего-н. с точки зрения величины, размеров, количества содержащегося. О. работ. О. знаний. Поставить проблему во всем объеме. ◊

объе́м, -ся, объешь, -ся. Буд. вр. от объесть, -ся.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

объём

1. мера занимаемого телом пространства, измеряемая в кубических единицах

3. трёхмерное тело ◆ Несколько объёмов пересекаются, образуя многогранник.

4. внутренняя часть тела ◆ Предполагается, что электронейтральность образца устанавливается за счет движения электронов с поверхности в объём по дислокациям. В. Д. Куликов, «Ток проводимости в структуре металл — диэлектрик — металл», 2004.10.15 г. // «Журнал технической физики» (цитата из НКРЯ)

5. разг. техн. то же, что рабочий объём поршневого двигателя внутреннего сгорания ◆ Бензиновый двигатель объёмом 1,4 л обеспечивает максимальную скорость 90 км/ч и запас хода 400 км. Владимир Мосалев, «Легкие боевые машины иностранных государств», 2004.08.04 г. // «Солдат удачи» (цитата из НКРЯ)

Фразеологизмы и устойчивые сочетания

• в полном объёме
• объём продаж
• объём производства
• объём работ
• рабочий объём

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова сегмент (существительное):

Значение термина «удельный»

Можно говорить о двух толкованиях, физическом и статистическом:

• В физике так называют величину, измеренную в единице чего-либо. Для примера возьмем комнату, и подсчитаем в ней количество водяного пара. Получив величину, А граммов, мы сможем сказать, что влажность здесь составляет, А граммов водяного пара на целую комнату. Зная общее количество воздуха в помещении (Б кг), мы можем найти, сколько воды содержится в одном килограмме воздуха, узнав его удельную влажность. В одном килограмме воздуха комнаты содержится А/Б г/кг водяного пара. Таким образом, синонимом термина выступает слово относительный.
• В статистических науках так называют частный показатель, взятый относительно некого целого. Для примера возьмем годовой бюджет страны, составляющий 500 млн, и вычислим долю расходов на спорт. Предположим, на спорт выделен 1 млн рублей — это 0,2% от всех планируемых трат. Не самая весомая статья бюджета.

Формула для гравитации

Математическое описание явления гравитации стало возможным благодаря многочисленным наблюдениям за движением космических тел. Результаты всех этих наблюдений в XVII веке обобщил Исаак Ньютон в рамках закона всемирного тяготения. Согласно этому закону, два тела, которые имеют массы m1 и m2, друг к другу притягиваются с такой силой F:

F = G * m1 * m2 / r2

Где r — расстояние между телами, G — некоторая постоянная.

Если в данное выражение подставить значение массы нашей планеты и ее радиус, тогда мы получим следующую формулу массы в физике:

Здесь F — сила тяжести, g — ускорение, с которым тела падают на землю вблизи ее поверхности.

Как известно, наличие силы тяжести обуславливает то, что все тела имеют вес. Многие путают вес и массу, полагая, что это одна и та же величина. Обе величины действительно связаны через коэффициент g, однако вес — величина изменчивая (она зависит от ускорения, с которым движется система). Кроме того, вес измеряется в ньютонах, а масса в килограммах.

Весы, которыми человек пользуется в быту (механические, электронные), показывают массу тела, однако измеряют его вес. Перевод между этими величинами является лишь вопросом калибровки прибора.

Примеры решения задач

Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.

Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.

Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.

Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

• V сохраняется при движениях.
• V удовлетворяет принципу Кавальери.
• Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
• Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

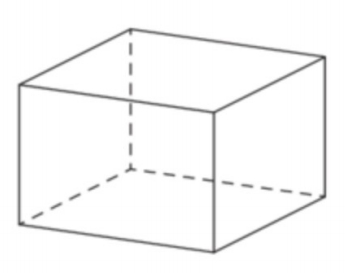
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

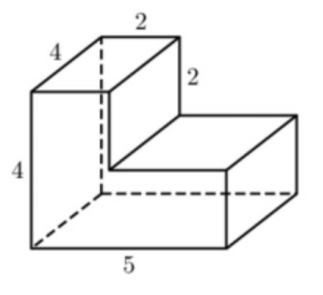
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

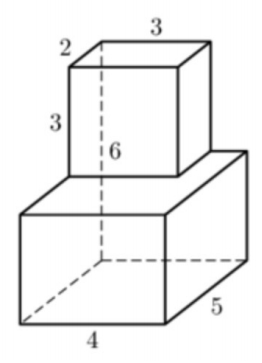
Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

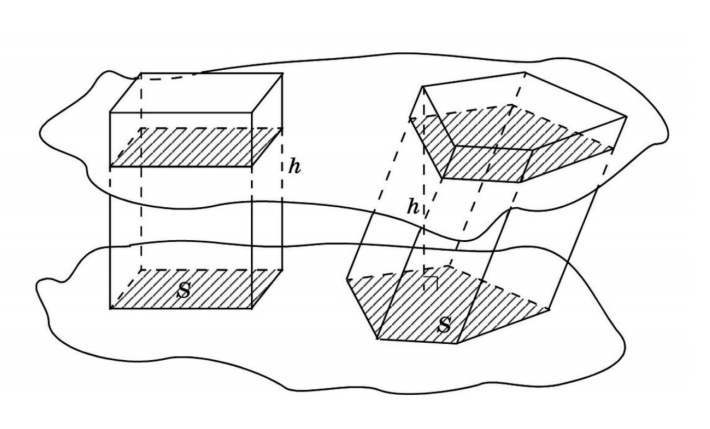
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

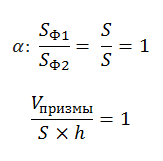
V S_осн h

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

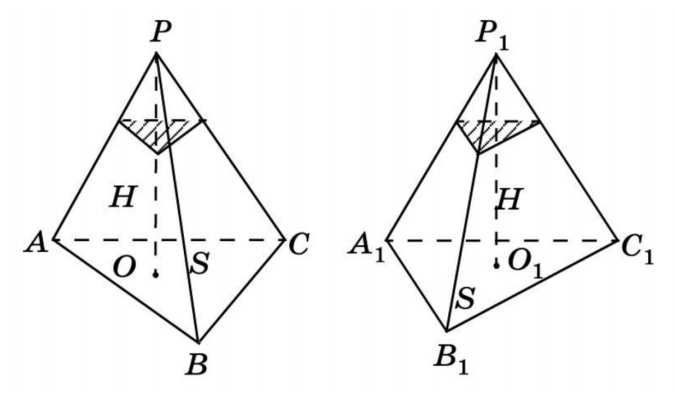
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V ₁/V₂ = 1 V₁ = V₂

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

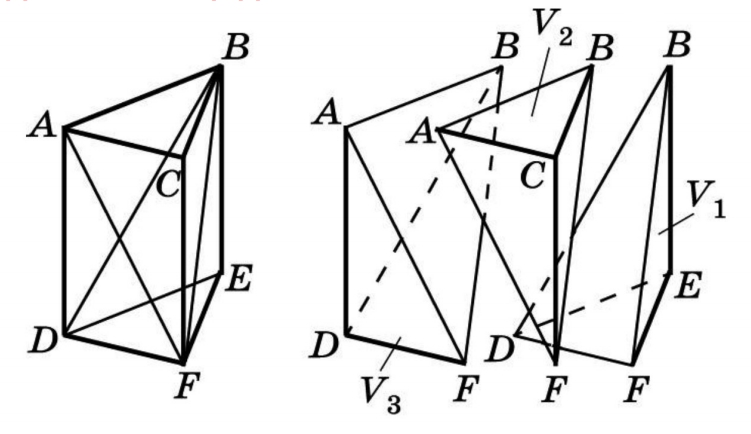
V_призмы S h = 3V

Объем цилиндра

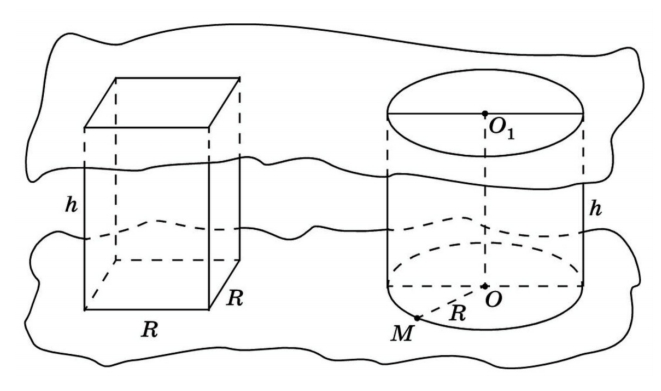
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

V_цил = πh × R 2

Объем конуса

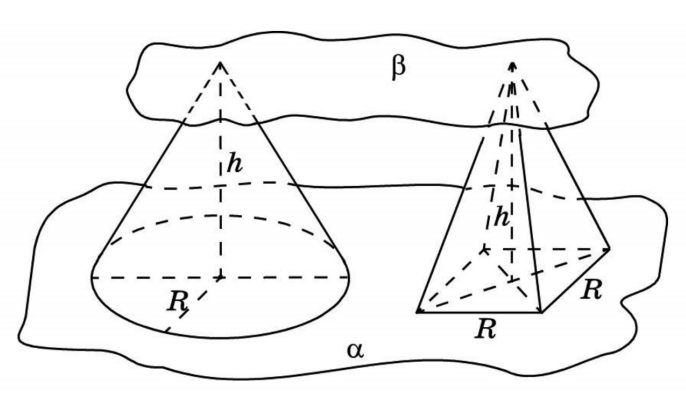
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

S_Ф1/S_Ф2 = π

V_конуса = 1/3 πR 2 h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте «Математические этюды» , где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR 2 . Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x 2 . Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R 2 — x 2 ).

Заметим, что: πR 2 + πR 2 — πR 2 = πR 2

V_цил = πR 2 × R = πR 3 = 1/3 R 3 π + V_шара

V_шара = 4/3 πR 3

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

Основные формулы термодинамики и молекулярной физики

Последняя тема в механике – это “Колебания и волны”:

Теперь можно смело переходить к молекулярной физике:

Плавно переходим в категорию, которая изучает общие свойства макроскопических систем. Это термодинамика:

Площадь и объем

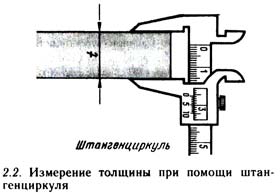
Измерьте длину l, ширину b и толщину t крышки стола в вашей лаборатории (рис. 2.1). Для длин более 15 см достаточную точность даст метровая (или полуметровая) линейка, проградуированная в мм. Например, для крышки стола длиной l = 108,0 см и шириной Ь = 92,6 см метровая линейка дает точность около 0,1%, грубо — 1:1000. Площадь рабо­чей поверхности А крышки стола составляет А = lb. Таким образом, А = (108,0) см х (92,6) см, или А = (1,08) м х (0,926) м, от­сюда А = 10 000,8 см 2 , или А= 1,000 08 м 2 . Заметьте, что в результате определения пло­щади А получили ответ, содержащий шесть значащих цифр, что составляет точность в 0,001%, грубо — 1 : 1 000 000. Поскольку ис­ходные измерения для l и Ь дали точность 1 : 1000, то такая точность не соответствует действительности. Ответ для А должен быть выражен как 10 000 см 2 , или 1,000 м 2 , т. е. до точности 1 : 1000. Это вычисление оставляет возможность для выбора, использовать ли нам см или м. Для вычисления площади А пред­ставляется, что использование метров (давать цифру 1,000 м) более предпочтительно.

Символом является греческая буква эта η. Но чаще все же используют выражение КПД.

Мощность механизма или устройства равна работе, совершаемой в единицу времени. Работа(A) измеряется в Джоулях, а время в системе Си – в секундах. Но не стоит путать понятие мощности и номинальной мощности. Если на чайнике написана мощность 1 700 Ватт, это не значит, что он передаст 1 700 Джоулей за одну секунду воде, налитой в него. Это мощность номинальная. Чтобы узнать η электрочайника, нужно узнать количество теплоты(Q), которое должно получить определенное количество воды при нагреве на энное количество градусов. Эту цифру делят на работу электрического тока, выполненную за время нагревания воды.

Величина A будет равна номинальной мощности, умноженной на время в секундах. Q будет равно объему воды, умноженному на разницу температур на удельную теплоемкость. Потом делим Q на A тока и получаем КПД электрочайника, примерно равное 80 процентам. Прогресс не стоит на месте, и КПД различных устройств повышается, в том числе бытовой техники.

Напрашивается вопрос, почему через мощность нельзя узнать КПД устройства. На упаковке с оборудованием всегда указана номинальная мощность. Она показывает, сколько энергии потребляет устройство из сети. Но в каждом конкретном случае невозможно будет предсказать, сколько конкретно потребуется энергии для нагрева даже одного литра воды.

Например, в холодной комнате часть энергии потратится на обогрев пространства. Это связано с тем, что в результате теплообмена чайник будет охлаждаться. Если, наоборот, в комнате будет жарко, чайник закипит быстрее. То есть КПД в каждом из этих случаев будет разным.

Относительная влажность воздуха, количество теплоты

Насыщенные и ненасыщенные пары

Насыщенный пар

При испарении одновременно с переходом молекул из жидкости в пар происходит и обратный процесс. Беспорядочно двигаясь над поверхностью жидкости, часть молекул, покинувших ее, снова возвращается в жидкость.

Если испарение происходит в закрытом сосуде, то сначала число молекул, вылетевших из жидкости, будет больше числа молекул, возвратившихся обратно в жидкость. Поэтому плотность пара в сосуде будет постепенно увеличиваться. С увеличением плотности пара увеличивается и число молекул, возвращающихся в жидкость. Довольно скоро число молекул, вылетающих из жидкости, станет равным числу молекул пара, возвращающихся обратно в жидкость. С этого момента число молекул пара над жидкостью будет постоянным. Для воды при комнатной температуре это число приблизительно равно $10^<22>$ молекул за $1с$ на $1см^2$ площади поверхности. Наступает так называемое динамическое равновесие между паром и жидкостью.

Пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным паром.

Это означает, что в данном объеме при данной температуре не может находиться большее количество пара.

При динамическом равновесии масса жидкости в закрытом сосуде не изменяется, хотя жидкость продолжает испаряться. Точно так же не изменяется и масса насыщенного пара над этой жидкостью, хотя пар продолжает конденсироваться.

Давление насыщенного пара. При сжатии насыщенного пара, температура которого поддерживается постоянной, равновесие сначала начнет нарушаться: плотность пара возрастет, и вследствие этого из газа в жидкость будет переходить больше молекул, чем из жидкости в газ; продолжаться это будет до тех пор, пока концентрация пара в новом объеме не станет прежней, соответствующей концентрации насыщенного пара при данной температуре (и равновесие восстановится). Объясняется это тем, что число молекул, покидающих жидкость за единицу времени, зависит только от температуры.

Итак, концентрация молекул насыщенного пара при постоянной температуре не зависит от его объема.

Поскольку давление газа пропорционально концентрации его молекул, то и давление насыщенного пара не зависит от занимаемого им объема. Давление $р_0$, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара.

При сжатии насыщенного пара большая его часть переходит в жидкое состояние. Жидкость занимает меньший объем, чем пар той же массы. В результате объем пара при неизменной его плотности уменьшается.

Зависимость давления насыщенного пара от температуры. Для идеального газа справедлива линейная зависимость давления от температуры при постоянном объеме. Применительно к насыщенному пару с давлением $р_0$ эта зависимость выражается равенством:

Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры.

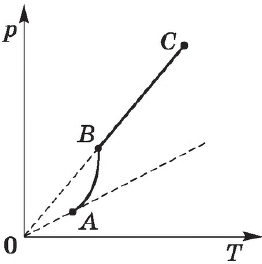
Экспериментально определенная зависимость $Р_0(Т)$ отличается от зависимости $p_0=nkT$ для идеального газа. С увеличением температуры давление насыщенного пара растет быстрее, чем давление идеального газа (участок кривой $АВ$). Это становится особенно очевидным, если провести изохору через точку $А$ (пунктирная прямая). Происходит это потому, что при нагревании жидкости часть ее превращается в пар, и плотность пара растет.

Поэтому, согласно формуле $p_0=nkT$, давление насыщенного пара растет не только в результате повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара. Главное различие в поведении идеального газа и насыщенного пара заключается в изменении массы пара при изменении температуры при неизменном объеме (в закрытом сосуде) или при изменении объема при постоянной температуре. С идеальным газом ничего подобного происходить не может (МКТ идеального газа не предусматривает фазового перехода газа в жидкость).

После испарения всей жидкости поведение пара будет соответствовать поведению идеального газа (участок $ВС$ кривой).

Ненасыщенный пар

Если в пространстве, содержащем пары какой-либо жидкости, может происходить дальнейшее испарение этой жидкости, то пар, находящийся в этом пространстве, является ненасыщенным.

Пар, не находящийся в состоянии равновесия со своей жидкостью, называется ненасыщенным.

Ненасыщенный пар можно простым сжатием превратить в жидкость. Как только это превращение началось, пар, находящийся в равновесии с жидкостью, становится насыщенным.

Влажность воздуха

Влажность воздуха — это содержание в воздухе водяного пара.

Окружающий нас атмосферный воздух вследствие непрерывного испарения воды с поверхности океанов, морей, водоемов, влажной почвы и растений всегда содержит в себе водяные пары. Чем больше водяных паров находится в определенном объеме воздуха, тем ближе пар к состоянию насыщения. С другой стороны, чем выше температура воздуха, тем большее количество водяных паров требуется для его насыщения.

В зависимости от количества водяных паров, находящихся при данной температуре в атмосфере, воздух бывает различной степени влажности.

Количественная оценка влажности

Для того чтобы количественно оценить влажность воздуха, пользуются, в частности, понятиями абсолютной и относительной влажности.

Абсолютная влажность — это количество граммов водяного пара, содержащееся в $1м^3$ воздуха при данных условиях, т. е. это плотность водяного пара $р$, выраженная в г/$м^3$.

Относительная влажность воздуха $φ$ — это отношение абсолютной влажности воздуха $р$ к плотности $р_0$ насыщенного пара при той же температуре.

Относительную влажность выражают в процентах:

Концентрация пара связана с давлением ($p_0=nkT$), поэтому относительную влажность можно определить как процентное отношение парциального давления $р$ пара в воздухе к давлению $р_0$ насыщенного пара при той же температуре:

Под парциальным давлением понимают давление водяного пара, которое он производил бы, если бы все другие газы в атмосферном воздухе отсутствовали.

Если влажный воздух охлаждать, то при некоторой температуре находящийся в нем пар можно довести до насыщения. При дальнейшем охлаждении водяной пар начнет конденсироваться в виде росы.

Точка росы

Точка росы — это температура, до которой должен охладиться воздух, чтобы находящийся в нем водяной пар достиг состояния насыщения при постоянном давлении и данной влажности воздуха. При достижении точки росы в воздухе или на предметах, с которыми он соприкасается, начинается конденсация водяного пара. Точка росы может быть вычислена по значениям температуры и влажности воздуха или определена непосредственно конденсационным гигрометром. При относительной влажности воздуха $φ = 100%$ точка росы совпадает с температурой воздуха. При $φ t_1$ и, следовательно, $Q > 0$. При охлаждении тела $t_2