Как узнать площадь комнаты

Чтобы рассчитать площадь помещения, достаточно иметь минимальный набор инструментов и знаний на уровне 5-го класса. Под рукой должны быть рулетка, карандаш и лист бумаги. Для определения площади необходимо длину умножить на ширину.

Важно! Стоит понимать, что эта формула действует только для идеально квадратной или прямоугольной квартиры, для сложной конфигурации есть свои проблемы, как и для тех квартир, в стенах которых предполагаются ниши.

Что такое 1 см² и 1 м²

По сути, любую фигуру можно измерить в миллиметрах, сантиметрах, метрах и т.д. Если это значение в «квадрате», т.е. мм2, см2, м2 и т.д., то это говорит о том, что площадь измеряется в количестве квадратов, каждая сторона из которых равна одноименному значению – 1 мм2, 1 см2, 1 м2 и т.д. В строительстве берется за основу 1 м2.

Формулы

Чтобы узнать, как вычислить площадь комнаты в м2, достаточно провести несложные арифметические вычисления. Для этого просто измерить ее длину и ширину, потом сложить получившееся значение и умножить на 2: к примеру возьмем размер 160 см на 100 см. Умножаем цифры 160 на 100 и получаем 16000 см в квадрате.

Можно поступить еще проще и просто все стороны помещения перемножить: потолок, пол, стены.

Перевод квадратных сантиметров в квадратные метры

Перед тем, как узнать сколько в комнате квадратных метров, очень важно разобраться в самих значениях, ведь когда идет расчет с сотнями сантиметров, их в любом случае необходимо переводить в метры. Делается это по следующей формуле, уже на известном примере: 160 см * 100 см – разница величин (в одном метре – 100 сантиметров), в итоге получается 16000 см2, которые нужно разделить на 10000 и получим = 1.60 м2.

Такими цифрами намного проще оперировать и запоминать. Тем более, что «квадратуру» помещения всегда измеряют именно в метрах. Для перевода необходимо подставлять следующие формулы:

• 8000 см² / 10000 = 0,8 м²;
• 34000 см² / 10000 = 3,4 м²;
• 2400 см²/ 10000 = 0,24 м².

Все достаточно просто и не составит труда составить такие несложные арифметические вычисления, даже школьнику. Очень важно перед тем, как узнать квадратуру комнаты, провести максимально точные измерения, после чего приступить к расчетам.

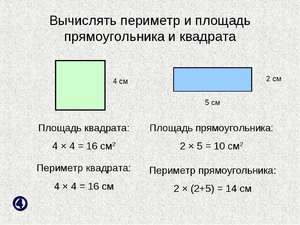
Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a 2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

• высота потолков;
• высота и ширина дверных проемов;
• высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

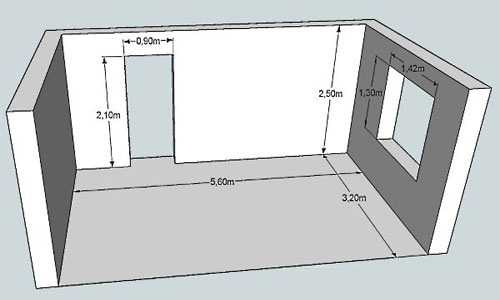
Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

1. Стена с дверью:
   • 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
   • сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
   • стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
2. Стена с окном:
   1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
   2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,75 кв.м.
   3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Как перевести площадь из одной единицы в другую

Еди­ни­ца пло­ща­ди пред­став­ля­ет собой линей­ную еди­ни­цу дли­ны, воз­ве­ден­ную в квад­рат.

Боль­шин­ство ЕИ могут быть как линей­ны­ми, так и квад­рат­ны­ми вели­чи­на­ми:

• линей­ные исполь­зу­ют­ся для опре­де­ле­ния раз­ме­ров объ­ек­тов и рас­сто­я­ний;
• квад­рат­ные — для изме­ре­ния пло­ща­дей гео­мет­ри­че­ских фигур, поме­ще­ний, зда­ний, земель­ных участ­ков.

Но такие меры, как акр, ар и гек­тар, не име­ют линей­ных ана­ло­гов и отно­сят­ся к чисто земель­ным мерам.

Краткая историческая справка

Рас­смот­рим исто­рию неко­то­рых еди­ниц изме­ре­ния пло­ща­ди.

• Про­ис­хож­де­ние земель­ной меры — акра име­ет забав­ную исто­рию. Изна­чаль­но акр обо­зна­чал раз­мер земель­но­го участ­ка, кото­рый мог обра­бо­тать за день один кре­стья­нин, исполь­зуя тяг­ло­вую силу одно­го вола.
• Миля берет своё нача­ло в древ­нем Риме. Она рав­ня­лась тыся­че двой­ных шагов, сде­лан­ных во вре­мя мар­ша вои­на­ми, оде­тых в пол­ное бое­вое обла­че­ние.

Какие земельные меры применяются в России

В Рос­сии в каче­стве земель­ных мер при­ме­ня­ют­ся в основ­ном сле­ду­ю­щие ЕИ пло­ща­ди:

• гек­тар (га);
• квад­рат­ный метр (м2);
• ар/сотка (а).

Гек­тар и квад­рат­ный метр вклю­че­ны в насто­я­щее вре­мя в меж­ду­на­род­ную систе­му еди­ниц СИ и име­ют соот­вет­ству­ю­щее обо­зна­че­ние: ha и mm 2 .

• В РФ гек­тар исполь­зу­ет­ся для изме­ре­ния пло­ща­дей земель­ных наде­лов с целе­вым назна­че­ни­ем — сель­ское или лес­ное хозяй­ство. Гек­тар — это квад­рат, сто­ро­на кото­ро­го рав­на 100 м или 0,1 км.
• Квад­рат­ный метр может иметь повсе­мест­ное при­ме­не­ние как меж­ду­на­род­ная систем­ная еди­ни­ца. Исполь­зу­ет­ся для опре­де­ле­ния пло­ща­ди ком­нат, квар­тир, зда­ний, постро­ек, земель­ных наде­лов назна­че­ния под насе­лен­ные пунк­ты и т.д. Один м 2 пред­став­ля­ет собой пло­щадь квад­ра­та со сто­ро­ной, рав­ной 1 м.
• Ар (сот­ка) сего­дня офи­ци­аль­но прак­ти­че­ски не упо­треб­ля­ет­ся, но в оби­хо­де до сих пор встре­ча­ет­ся доволь­но часто в каче­стве еди­ни­цы пло­ща­ди земель­но­го участ­ка под ИЖС. Один ар равен пло­ща­ди квдр. со сто­ро­ной 10 м, то есть 100 м 2 . (Отсю­да обра­зо­вал­ся и сам тер­мин “сот­ка”).

Меж­ду тре­мя земель­ны­ми мера­ми такая связь: 1 ha = 10000 м 2 (0,01 км 2 ) = 100 a (соток).

Таблицы перевода единиц измерения

Пере­ве­сти одни ЕИ пло­ща­ди в дру­гие мож­но, исполь­зуя раз­лич­ные таб­ли­цы пере­во­да и неслож­ный рас­чёт.

Напри­мер, нуж­но пере­ве­сти 700 аров в гек­та­ры. Состав­ля­ем про­пор­цию:

х = 700/100 = 7 га.

Ответ: 700 аров (соток) рав­ны 7 га.

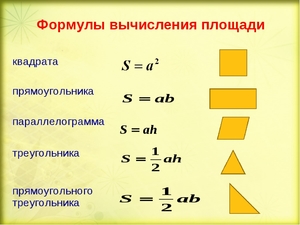
Формулы расчета

Зная площади простых фигур, можно находить параметры более сложных. Античными математиками были выведены формулы, по которым можно легко их вычислять. Такими фигурами являются треугольник, четырёхугольник, многоугольник, круг.

Чтобы найти площадь сложной плоской фигуры, её разбивают на множество простых фигур, таких как треугольники, трапеции или прямоугольники. Затем математическими методами выводят формулу для площади этой фигуры. Подобный метод используют не только в геометрии, но и в математическом анализе для вычисления площадей фигур, ограниченных кривыми.

Треугольник

Начнём с самой простой фигуры — треугольника. Они бывают прямоугольные, равнобедренные и равносторонние. Возьмём любой треугольник ABC со сторонами AB=a, BC=b и AC=c (∆ ABC). Чтобы найти его площадь, вспомним известные из школьного курса математики теоремы синусов и косинусов. Отпуская все выкладки, придём к следующим формулам:

• S=√[p•(p-a)•(p-b)•(p-c)] — известная всем формула Герона, где p=(a+b+c)/2 — полупериметр треугольника;
• S=a•h/2, где h — высота, опущенная на сторону a;
• S=a•b•(sin γ)/2, где γ — угол между сторонами a и b;
• S=a•b/2, если ∆ ABC — прямоугольный (здесь a и b — катеты);
• S=b²•(sin (2•β))/2, если ∆ ABC — равнобедренный (здесь b — одно из «бёдер», β — угол между «бёдрами» треугольника);
• S=a²•√¾, если ∆ ABC — равносторонний (здесь a — сторона треугольника).

Четырёхугольник

Пусть имеется четырёхугольник ABCD, у которого AB=a, BC=b, CD=c, AD=d. Чтобы найти площадь S произвольного 4-угольника, нужно разделить его диагональю на два треугольника, площади которых S1 и S2 в общем случае не равны.

Затем по формулам вычислить их и сложить, т. е. S=S1+S2. Однако, если 4-угольник принадлежит к определённому классу, то его площадь можно найти по заранее известным формулам:

• S=(a+c)•h/2=e•h, если 4-угольник — трапеция (здесь a и c — основания, e — средняя линия трапеции, h — высота, опущенная на одно из оснований трапеции;
• S=a•h=a•b•sin φ=d1•d2•(sin φ)/2, если ABCD — параллелограмм (здесь φ — угол между сторонами a и b, h — высота, опущенная на сторону a, d1 и d2 — диагонали);
• S=a•b=d²/2, если ABCD — прямоугольник (d — диагональ);
• S=a²•sin φ=P²•(sin φ)/16=d1•d2/2, если ABCD — ромб (a — сторона ромба, φ — один из его углов, P — периметр);
• S=a²=P²/16=d²/2, если ABCD — квадрат.

Многоугольник

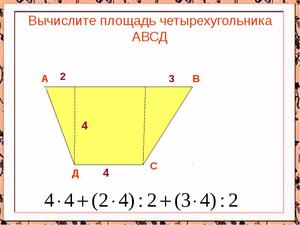Чтобы найти площадь n-угольника, математики разбивают его на простейшие равные фигуры —треугольники, находят площадь каждого из них и затем складывают. Но если многоугольник относится к классу правильных, то используют формулу:

S=a•n•h/2=a²•n/[4•tg (180°/n)]=P²/[4•n•tg (180°/n)], где n — количество вершин (или сторон) многоугольника, a — сторона n-угольника, P — его периметр, h — апофема, т. е. отрезок, проведённый из центра многоугольника к одной из его сторон под углом 90°.

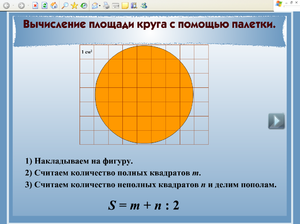Круг — это совершенный многоугольник, имеющий бесконечное число сторон. Нам необходимо вычислить предел выражения справа в формуле площади многоугольника при числе сторон n, стремящемуся к бесконечности. В этом случае периметр многоугольника превратится в длину окружности радиуса R, которая будет границей нашего круга, и станет равен P=2•π•R. Подставим это выражение в указанную выше формулу. Мы получим:

Найдём предел этого выражения при n→∞. Чтобы это сделать, учтём, что lim (cos (180°/n)) при n→∞ равен cos 0°=1 (lim — знак предела), а lim [1/(n•sin (180°/n))]= lim [1/(n•sin (π/n))] при n→∞ равен 1/π (мы перевели градусную меру в радианную, используя соотношение π рад=180°, и применили первый замечательный предел lim (sin x)/x=1 при x→∞). Подставив в последнее выражение для S полученные значения, придём к известной формуле:

История возникновения понятия «1 сотка»

В дореволюционной России для измерений участков земли использовали такое понятие, как десятины. После 1917г. они были заменены на ары. Таким образом ар представляет собой квадрат 10х10 м с общей площадью 100м 2 .

Введение этой величины упростило процесс подсчета площади участка. Размер участка определялся количеством квадратов 10х10 м, из которых он состоял. Вскоре архаический ар был вытеснен понятной в употреблении соткой. Теперь понять, сколько метров квадратных в сотке земли, стало намного проще исходя из самого определения: сотка – это сто метров.

Существует еще одна версия, как возникло понятие сотка. Некоторые считают, что термин обозначает сотую часть гектара: 1 га=10 000 кв. м / 100. В любом случае сотки применяются и по настоящее время и важны в некоторых аспектах землевладения.

Всем известно понятие 6 соток для сельского хозяйства. Однако 6 соток – это сколько метров для хозяйства? По факту это 600 м 2 , которыми наделялась семья из четырех человек в период, известный в истории страны как период планирования (1960-1970гг). Этого количества земли должно было хватить на выращивание овощей и фруктов с 5 соток, а на 6-й сотке планировалось строительство дачного жилого домика и хозяйственных построек, не более 2-х. Эта величина считается средней по величине и в наши дни.

Понятие сотка настолько укоренилось для обозначения площади участка, и это стало не столько простонародным, но и закрепилось в бумагах. Например, можно увидеть объявление о продаже участка с указанием 6 соток, а не квадратных метров.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

• Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
• Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
• Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

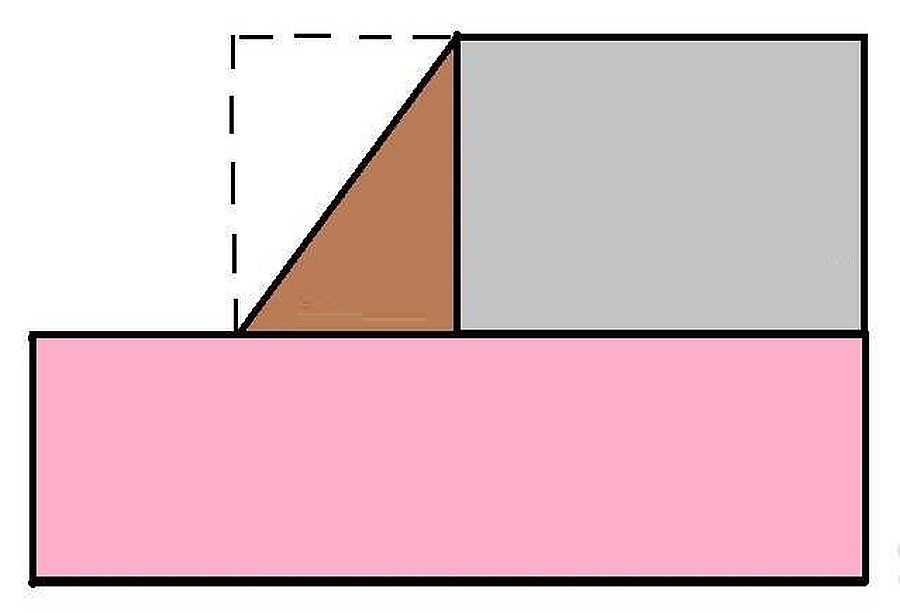Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

• Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
• Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Снова округлим до 0,67 м².
• Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
• Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

Варианты обозначения

Понятие используется не только в математике. Оно актуально и для физики.

В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.

В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.

В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение <�эс>.

Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.

Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.

Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.

Интересно! Что значит вертикально и как выглядит вертикальная линия

Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.

Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.

Советы и рекомендации

Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.

Совет! При расчетах лучше пригласить еще одного человека в помощь. Одна голова хорошо, а две надежнее.

Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.

Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.

Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.

Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин. В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.