Пружинный маятник; формулы и уравнения нахождения величин

Пружинный маятник – формулы и уравнения нахождения величин

Пружинный маятник – колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики.

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид:

где $<�щu>^2_0=frac$ — циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

где $_0=sqrt>>0$- циклическая частота колебаний маятника, $A$ — амплитуда колебаний; $<(omega >_0t+varphi )$ — фаза колебаний; $varphi $ и $_1$ — начальные фазы колебаний.

В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde=Releft(Acdot exp left(ileft(_0t+varphi right)right)right)left(3right).]

Свободные колебания

Уравнение вида x ¨ + ω 0 2 x = 0 получило название уравнения свободных колебаний. Их физические свойства могут определять только собственную частоту колебаний ω 0 или период Т .

Амплитуда x m и начальная фаза φ 0 находят при помощи способа, который вывел их из состояния равновесия начального момента времени.

При наличии смещенного груза из положения равновесия на расстояние ∆ l и моменте времени, равном t = 0 , производится его опускание без начальной скорости. Тогда x m = ∆ l , φ 0 = 0 . Если груз находился в положении равновесия, то при толчке передается начальная скорость ± υ 0 , отсюда x m = m k υ 0 , φ 0 = ± π 2 .

Амплитуда x m с начальной фазой φ 0 определяются наличием начальных условий.

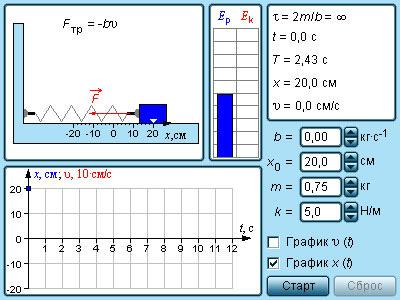
Рисунок 2 . 2 . 2 . Модель свободных колебаний груза на пружине.

Механические колебательные системы отличаются наличием сил упругих деформаций в каждой из них. Рисунок 2 . 2 . 2 показывает угловой аналог гармонического осциллятора, совершающий крутильные колебания. Диск располагается горизонтально и висит на упругой нити, закрепленной в его центре масс. Если его повернуть на угол θ , тогда возникает момент силы упругой деформации кручения M у п р :

Данное выражение не соответствует закону Гука для деформации кручения. Величина x аналогична k жесткости пружины. Запись второго закона Ньютона для вращательного движения диска принимает вид

I ε = M у п р = — x θ или I θ ¨ = — x θ , где моментом инерции обозначается I = I C , а ε – угловое ускорение.

Аналогично с формулой пружинного маятника:

ω 0 = x I , T = 2 π I x .

Применение крутильного маятника замечено в механических часах. Он получил название балансира, в котором создание момента упругих сил производится при помощи спиралевидной пружины.

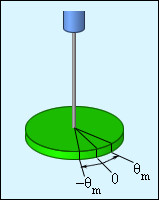
Рисунок 2 . 2 . 3 . Крутильный маятник.

Уравнение движения пружинного маятника

Пусть начало координат находится в точке покоя маятника. Тогда, если маятник выведен из состояния равновесия на расстояние $x$, со стороны пружины на него начинает действовать сила $F=-kx$.

Согласно второму закону Ньютона, если на тело действует сила, то оно приобретает ускорение:

Скорость – это производная координаты. А ускорение – производная скорости. Следовательно, ускорение – это вторая производная координаты. Получим уравнение:

То есть, вторая производная координаты пропорциональна самой координате, взятой с противоположным знаком. Это дифференциальное уравнение, и в высшей математике доказывается, что единственная функция, являющаяся его решением – это круговая функця (синус или косинус).

Если взять вторую производную этой функции, то можно убедиться, что она равна самой себе, с противоположным знаком и необходимым коэффициентом.

Задача может поначалу удивить тем, что в ней как будто ничего и не дано, а что-то при этом требуется доказать. Но ничего страшного тут нет. Когда задача формулируется таким образом, это означает, что вы можете для себя ввести какие-то обозначения, которые вам нужны, сосчитать с ними то, что требуется, а потом прийти к выводу, который уже не зависит от этих величин. Проделайте это для данной задачи. Возьмите формулы для периодов колебания, подумайте, что за величины в них входят, и сравните два периода друг с другом, поделив один на другой.

Период колебания грузика массы m на пружинке жесткости k и длины L составляет

.

Эта формула не меняется и в том случае, если грузик подвешен в поле тяжести с ускорением свободного падения g. Конечно, положение равновесия грузика сместится вниз на высоту ΔL = mg/k — именно при таком удлинении пружинки сила упругости компенсирует силу тяжести. Но период вертикальных колебаний относительно этого нового положения равновесия с растянутой пружинкой останется тем же.

Период горизонтальных колебаний растянутого маятника выражается через ускорение свободного падения g и его полную длину L = L + ΔL:

.

Именно благодаря дополнительному растяжению в поле тяжести мы выясняем, что

Вот и всё решение.

Разновидности пружинного маятника

Для периода колебаний пружинного маятника возможно выделить несколько основных видов конструкции. Главные различия заключаются в виде установленной пружины. Среди главных особенностей можно выделить:

1. Распространение есть у вертикальной амплитуды груза на пружине, так как на него не распространяется сила трения и прочие воздействия. Возрастает степень влияния силы тяжести. Благодаря этому существует вероятность того, что в начальной точке тело способно совершить значительное число движений инерционного характера.
2. Горизонтальный маятник также имеет распространение. Груз располагается на опорной поверхности, при передвижениях происходит трение. Широкое применение механизм нашел в кинематических задачах по физике.
3. В качестве пружины используется стандартная витковая разновидность. В этом случае имеется некоторое пространство под названием шаг. Концевые витки выполняются в форме плоскости, что позволяет равномерным образом распределить кинетическое усилие.
4. Также может быть поставлена пружина для растягивания. Это происходит в том случае, если прикладываемое усилие оказывается причиной для роста длины. Закрепление происходит за счет крючков.

Все описанные варианты имеют распространение. Важно учесть, что сила должна быть приложена параллельно оси. Иначе возможно возникновение значительных дефектов, одним из которых является деформация.

Свойства маятника

У маятника есть ряд интересных свойств, подтвержденных физическими законами. Так период колебаний всякого маятника зависит от таких факторов, как его размер, форма тела, расстояние между центром тяжести и точкой подвеса. Поэтому определение периода маятника является не простой задачей. А вот период математического маятника можно рассчитать точно по формуле, которая будет приведена ниже.

В ходе наблюдений за маятниками были выведены следующие закономерности:

• Если к маятнику подвешивать разные грузы с разным весом, но при этом сохранять одинаковую длину маятника, то период его колебания будет одинаковым вне зависимости от массы груза.
• Если при запуске колебаний отклонить маятник на не очень большие, но все же разные углы, то он станет колебаться в одинаковым период, но по разным амплитудам. Следовательно, период колебания у подобного маятника не зависит от амплитуды колебания, такое явление было названо изохронизмом, что с древнегреческого можно перевести как «хронос» – время, «изо» – равный, то есть «равновременный».

Уравнение гармонических колебаний

1. Гармонические колебания как простейший периодический процесс
2. Перемещение, скорость и ускорение при гармоническом движении
3. Примеры

п.1. Гармонические колебания как простейший периодический процесс

Например:
1) Вращение Луны вокруг Земли, Земли и других планет вокруг Солнца, Солнечной системы в целом вокруг центра Галактики;
2) Колебания атомов в молекуле, колебания электромагнитного поля;
3) Сокращения сердечной мышцы, колебания маятника часов, движение поршня в двигателе внутреннего сгорания, смена дня и ночи, приливы и отливы.

Например:
1) Период вращения минутной стрелки часов T=1 час
Период вращения Земли вокруг своей оси T=1 сут=24 ч
Период вращения Земли вокруг Солнца T=1 год=365 сут
2) Период колебаний атомов в двухатомных молекулах T=10 -14 с
Период вращения Солнца вокруг центра Галактики T=240 млн.лет.≈7,6·10 15 с

Если состояние системы характеризуется некоторой функцией от времени (s=x(t)), то для периодического процесса выполняется равенство: (x(t+T)=x(t)).
Простейшими периодическими функциями являются тригонометрические функции (sin⁡t) и (cos⁡t) с периодом (T=2pi).

Множитель (omega) перед аргументом (t) тригонометрической функции сокращает её период в (omega) раз (см. §8 данного справочника). Поэтому:

Например:
Запишем закон колебаний математического маятника – шарика на нити, если в начальный момент времени он был отклонен на 5 см, а затем отпущен. При подсчете за 10 с он совершил 20 колебаний.
Отклонение в начальный момент соответствует амплитудному значению A=5 см при (t_0=0), значит, будем описывать колебания по закону косинуса с начальной фазой (varphi_0=0). По условию за t=10 с зафиксировано N=20 колебаний, откуда частота: begin nu=frac Nt, omega=2pinu=2pifrac Nt\ omega=2picdotfrac<20><10>=4pi text <�рад/с>end Получаем закон колебаний: (x(t)=5cos(4pi t))

п.2. Перемещение, скорость и ускорение при гармоническом движении

Пусть (x(t)) — координата тела, участвующего в периодическом движении по закону: $ x(t)=Acos⁡omega t $ Найдем скорость как первую производную от координаты: $ v(t)=x'(t)=-Aomega sinomega t=Aomega cos⁡left(omega t+fracpi 2right) $ Мы видим, что колебания скорости происходят с той же частотой, что и колебания координаты, но опережают их по фазе на (fracpi 2). Амплитудное значение скорости: $ v_m=Aomega $ Найдем ускорение как первую производную от скорости (и соответственно, вторую производную от координаты): $ a(t)=v'(t)=x»(t)=-Aomega^2 cosomega t=Aomega^2 cos⁡(omega t+pi) $ Колебания ускорения также происходят с той же частотой, опережая колебания скорости на (fracpi 2) и колебания координаты на (pi). Амплитудное значение ускорения: $ a_m=Aomega^2 $ Например:
При A=2 и (omega=frac12) получаем такие синусоиды:

Из уравнения для ускорения получаем: $ x»(t)=-Aomega^2cosomega t=-omega^2(Acosomega t)=-omega^2 x(t) $ Откуда следует:

Решением этого уравнения в общем виде будут: $ x(t)=Asin⁡(omega t+varphi_0) text<�или> x(t)=A cos⁡(omega t+varphi_0) $ Для каждой из систем физический смысл (x(t)) и (omega) будет разным.

п.3. Примеры

Пример 1. Получите уравнение гармонических колебаний для горизонтального пружинного маятника с массой m и жесткостью пружины k. Чему равна циклическая частота этих колебаний?

Горизонтальный пружинный маятник – это грузик массой m, прикрепленный к пружине жесткостью k. Грузик может перемещаться в горизонтальном направлении без трения.

По вертикали на грузик действую сила тяжести и реакция опоры, равнодействующая которых равна нулю.
По горизонтали на грузик действует только сила упругости: (F=-kcdot x(t))
Самое время вспомнить о втором законе Ньютона. Сила, действующая на грузик, приводит его в движение с ускорением a: begin F=ma=mcdot x»(t)\ mcdot x»(t)=-kcdot x(t) end Уравнение движения грузика: $ x»(t)+frac km x(t)=0 $ что является уравнением гармонических колебаний с частотой: (omega=sqrt)
Общее решение уравнения: (x(t)=Acosleft(sqrt+varphi_0right))
Амплитудные значения скорости и ускорения: $ v_m=Asqrt, a_m=Afrac km $ Ответ: (omega=sqrt)

Пример 2. Получите уравнение гармонических колебаний для малых углов отклонений математического маятника на нити длиной l при ускорении свободного падения g. Чему равна циклическая частота этих колебаний?

Математический маятник – это шарик, который можно считать материальной точкой, на длинной невесомой нерастяжимой нити длиной l в поле тяготения с ускорением свободного падения g.

Пример 3. Получите уравнение гармонических колебаний для L-контура.
Чему равна циклическая частота этих колебаний?

LC-контур – это электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C. Модель является идеальной, т.к. предполагает, что в цепи полностью отсутствует активное сопротивление R, и колебания не затухают со временем.

Напряжение на конденсаторе (U_C(t)=frac). Ток, протекающий через катушку, создает ЭДС (varepsilon_L(t)=-Lfrac). При переходе к пределу (triangle trightarrow 0) получаем производную (varepsilon_L(t)=-LI'(t)). По второму закону Кирхгофа для замкнутого контура: begin U_c(t)=varepsilon_L(t)Rightarrow frac=-LI'(t)Rightarrow frac+LI'(t)=0 end Вспомним, что (Q'(t)=I(t)) – ток равен производной от заряда по времени.
Тогда первая производная от тока равна второй производной от заряда (I'(t)=Q»(t)).
begin frac+LQ»(t)=0 end Получаем уравнение гармонических колебаний: $ Q»(t)=frac<1>Q(t)=0, omega=frac<1>> $ Общее решение уравнения: (Q(t)=Q_m cosleft(frac<1>>t+varphi_0right))
Напряжение на конденсаторе: $ U_C(t)=frac=fraccosleft(frac<1>>t+varphi_0right) $ Амплитудное значение напряжения: (U_m=frac)
Ток как скорость изменения заряда: $ I(t)=Q'(t)=-frac>sinleft(frac<1>>t+varphi_0right)=frac>cosleft(frac<1>>t+varphi_0+fracpi 2right) $ Амплитудное значение тока: (I_m=frac>)
Ток опережает колебания заряда и напряжения на (fracpi 2)

Вектор силы (Определение, Пример)

Это то, что тянет и толкает; силы мы чувствуем, когда они на нас действуют; силы растягивают пружины, заставляют тело двигаться быстрее. Мы будем измерять силы при помощи пружинных весов. Поскольку эти приборы обычно градуируют в килограммах силы мы будем пока выражать силу тоже в килограммах силы.

При сооружении и проектировании мостов, зданий, кранов, машин инженеров очень заботит сложение сил или же разность сил для определения силы, необходимой для достижения равновесия. Можно показать, что силы — это векторы, т. е. они подчиняются правилу геометрического сложения.

Векторному сложению и разложению уравновешенных сил посвящен раздел физики, называемый «статикой». Это большой, но скучный раздел физики, и большинство учебников уделяет ему много места, излагая приемы решения задач инженерной статики. Мы ограничимся лишь несколькими примерами, и даже их, пожалуй, лучше было бы опустить, чтобы уделить больше времени изучению силы и движения.

Прежде всего мы должны удостовериться в том, что силы — это векторы. Сказать, что они должны быть векторами, поскольку они характеризуются величиной и направлением, недостаточно. Это не убеждает нас в том, что силы складываются геометрически.

Хотя это утверждение кажется вполне правдоподобным, особенно тем, кто имеет дело с канатами и веревками на кораблях или кому приходится заниматься разбивкой палаток, мы же должны проворить его непосредственно.

Опыт по определению вектора силы

Часто прибегают еще к одному способу проверки. Этот способ проще, но его косвенный характер порой (не совсем добросовестно) игнорируют. К узлу прикладывают две тянущие силы F_А и F_В (применяют гири и блоки или пружинные весы), а третья сила F_С удерживает узел в покое. Затем при помощи построения определяется сумма сил F_А и F_В .

Она равна и проти воположна силе F_С. Это требует дополнительного доказательства, поскольку F_С не равнодействующая (сумма) двух других сил, а «равновесная» сила, необходимая, чтобы им противостоять.

Рис. Косвенная проверка векторного сложения сил.

Равновесие сил

Если на какую-нибудь деталь крана или моста действует несколько сил сразу, а инженеру нужно, чтобы она была и оставалась в состоянии покоя, то для этого сумма всех действующих сил должна быть равна нулю. Тогда в соответствии с представлением Галилея эта деталь должна либо постоянно двигаться, либо постоянно оставаться в состоянии покоя.

В этом случае мы говорим, что силы находятся «в равновесии». Если сумма нескольких сил равна нулю, то это должно быть видно на диаграмме векторного сложения; длина линии, соединяющей исходную точку диаграммы с конечной, должна быть равна нулю. Это означает, что векторная диаграмма должна представлять собой замкнутую фигуру.

Таким образом, если сумма сил равна нулю, то конец векторного многоугольника должен прийти обратно к началу. Это иллюстрирует рис. 3. Условие равенства нулю равнодействующей для постоянного равновесия сил должно выполняться для всей конструкции, например для всего крана или моста, но оно должно также выполняться для каждой отдельной детали конструкции, находящейся в состоянии равновесия.

Применяя это условие к какой-нибудь определенной детали, например к стреле крана, к одной опоре моста, к заклепке, связывающей воедино несколько различных деталей моста, или к грузу маятника, нужно быть внимательным и учитывать все силы, действующие на данную деталь. Тогда мы сможем утверждать, что имеем полный набор сил, образующих замкнутую векторную диаграмму, если, конечно, деталь находится в равновесии.

При решении задач не следует включать в рассмотрение силы, приложенные к другим деталям. Сначала выберите и пометьте выбранную деталь, которая, как вы считаете, находится в равновесии.

Равновесие трех сил, треугольник сил

Если три силы находятся в равновесии, то их векторная диаграмма должна представлять собой замкнутый треугольник (рис. 4). Если известны две силы, то можно вычислить величину и направление третьей.

Рис. 4. Три силы.

а — три силы в равновесии) б — три силы не находятся в равновесии.

Этим пользуются при решении инженерных задач. Во многих конструкциях на каждую деталь, играющую важную роль, действуют как раз три силы. Чтобы конструкция была устойчивей, каждая деталь должна оставаться в состоянии покоя; сумма всех действующих на нее сил должна быть равна нулю. Таким образом, если к любой детали приложены три силы, мы строим для них замкнутый треугольник.